Vì \(f\left(b\right)\) đồng biến nên nếu \(f\left(-8\right)>0\Rightarrow f\left(b\right)>0;\forall b>-8\)

\(\Rightarrow f\left(b\right)\le0\) có nhiều nhất 3 nghiệm nguyên thuộc (-12;12) là -11;-10;-9 (ktm yêu cầu đề bài)

Do đó \(f\left(-8\right)\le0\)

Hiểu đơn giản thì đếm từ -11 trở đi thêm 4 số nguyên ta sẽ chạm tới mốc -8

=2(2x^3-3x^2+3x-1)

=2(2x^3-x^2-2x^2+x+2x-1)

=2(2x-1)(x^2-x+1)

tui chịu luôn đó

Câu 1 này bình phương hơi dài dòng nên khử trị tuyệt đối sẽ tốt hơn:

\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2-2x-3\ge0\\x^2-2x-3\ge3x-3\end{matrix}\right.\\\left\{{}\begin{matrix}x^2-2x-3< 0\\-\left(x^2-2x-3\right)\ge3x-3\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge3\\x\le-1\end{matrix}\right.\\x^2-5x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}-1< x< 3\\x^2+x-6\le0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge3\\x\le-1\end{matrix}\right.\\\left[{}\begin{matrix}x\ge5\\x\le0\end{matrix}\right.\end{matrix}\right.\\\left\{{}\begin{matrix}-1< x< 3\\-3\le x\le2\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge5\\x\le-1\end{matrix}\right.\\-1< x\le2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge5\\x\le2\end{matrix}\right.\)

Vậy C đúng

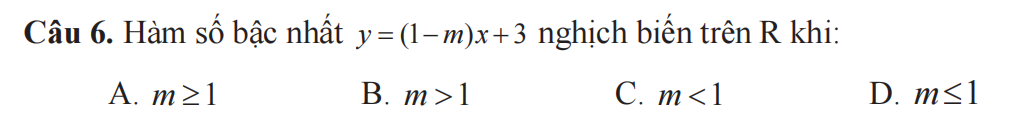
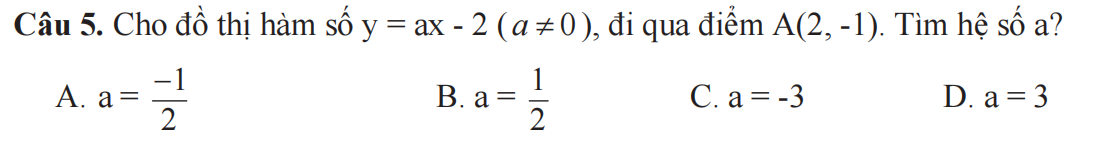
6.B

Hàm nghịch biến trên R khi:

\(1-m< 0\Rightarrow m>1\)

5.B

Đồ thị đi qua A nên:

\(-1=2a-2\Rightarrow2a=1\Rightarrow a=\dfrac{1}{2}\)

12.

\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)

\(\Rightarrow M=\sqrt{2}\)

13.

Pt có nghiệm khi:

\(5^2+m^2\ge\left(m+1\right)^2\)

\(\Leftrightarrow2m\le24\)

\(\Rightarrow m\le12\)

14.

\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)

\(\Leftrightarrow x=k2\pi\)

15.

\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)

Đáp án A

16.

\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)

\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)

Có \(1008+1008=2016\) nghiệm

Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0

=>m>1

=>Chọn B

Câu 7: D

Câu 10: (D)//(D')

=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

=>Chọn D

Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)

=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x

=>Chọn A

Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)

=>3m+2=2m+3

=>m=1

=>Chọn C

b c b c d d b d b d

TH1: thể 3 ở A, B, E

A-B-ddE- = 3.3.2.1.2 = 36

TH2: Thể 3 ở d

A-B-ddE- = 2.2.1.2 = 8

Tổng là 44