Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
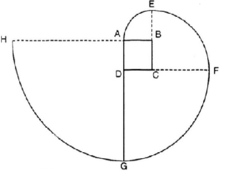
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.

Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
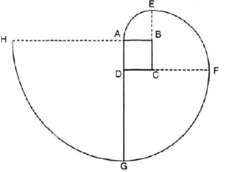
Hình 55
Cách vẽ:

Kiến thức áp dụng
+ Độ dài đường tròn đường kính d là: C = π.d
Cho hình vuông ABCD có độ dài cạnh là 10 cm . Gọi O là tâm đường tròn nội tiếp hình vuông. Gọi M, N lần lượt là trung điểm của AB; BC. Tính độ dài của cung M N ⏜ ?
A. 2 π (cm)
B. 5 π (cm)
C. 2,5 π (cm)
D. 7,5 π (cm)
Chọn đáp án C
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
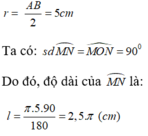
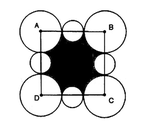
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm
A. 5.38
B. 7.62
C. 5.98
D. 4.44
Trên đường tròn bán kính R lần lượt đặt theo cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho
sd A B ^ = 60 ° , sd B C ^ = 90 ° và sd C D ^ = 120 °
a) Tứ giác ABCD là hình gì?
b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.
c) Tính độ dài các cạnh của tứ giác ABCD theo R.
b)
Gọi AC giao DB = I
Góc AIB có đỉnh I nằm trong đường tròn
\(\Rightarrow\widehat{AIB}=\frac{1}{2}.\left(sđ\widebat{AB}+sđ\widebat{CD}\right)\)
\(=\frac{1}{2}.\left(60^0+90^o\right)=90^o\)
=> AI vuông BI hay AC vuông BD ( đpcm )
c)
+) Tam giác OAB có :
OA = OB ; \(\widehat{AOB}=sđ\widebat{AB}=60^o\)
=> Tam giác OAB đều
=> AB = OA = OB = R
+) Tam giác OBC có \(\widehat{BOC}=sđ\widebat{BC}=90^o;OB=OC=R\)
- Áp dụng đlí Py - ta - go cho OBC , ta có :
\(BC^2=OB^2+OC^2=R^2+R^2=2R^2\)
\(\Rightarrow BC=R\sqrt{2}\)
+) ABCD là hình thang cân
\(\Rightarrow AD=BC=R\sqrt{2}\)
+) Gọi H là trung điểm của CD
Ta có : OD = OC
=> Tam giác OCD cân tại O
=> OH đồng thời là đường cao vừa là đường phân giác
Mà \(\widehat{DOC}=sđ\widebat{DC}=120^o\)
\(\Rightarrow\widehat{DOH}=\frac{1}{2}.\widehat{DOC}=60^o\)
Tam giác ODH vuông , áp dụng hệ thức về cạnh trong tam giác vuông , ta có :
\(DH=OD.\sin\widehat{DOH}=R.sin60^o=\frac{R\sqrt{3}}{2}\)
\(\Rightarrow CD=2.DH=R\sqrt{3}\)
a)Vẽ đường tròn tâm O, tâm C cùng đi qua A,2 đường tròn này cắt nhau tại D(khác A).Tính chu vi tam giác ABC đó
b)gọi m,N lần lượt là giao điểm của đường tròn tâm B,tâm C trên với cạnh BC. Tính độ dài MN
2.cho đường tròn tâm O và trên đó lấy 1 số điểm .Vẽ các dây có 2 mút là 2 trong số các điểm đã cho. Biết rằng có tất cả 78 dây
a)Tính số cung tạo thành
b)tính số điểm đã lấy trên đường tròn tâm O
cho hình vuông ABCD có độ dài cạnh bằn 1 dm vẽ hai đường tròn có bán kính bằng độ dài cạnh hình vuông có tâm lần lượt là A và C hãy tính diện tích còn lại
mau lên mình cho 6 like
Trên một tờ giấy có kẻ dòng, chọn khoảng cách giữa hai dòng làm đơn vị độ dài, vẽ 5 đường tròn cùng tâm I có bán kính lần lượt bằng 1, 2, 3, 4, 5 (đơn vị độ dài). Đánh dấu các đường tròn này theo thứ tự là (1), (2), (3), (4), (5). Trên một tờ giấy kính, kẻ hệ trục tọa độ Oxy, trên tia Oy lấy điểm K sao cho OK = ½ (đơn vị độ dài nói trên). Lấy điểm H(0 ; -1/2). Qua H kẻ đường thẳng Ht // Ox.
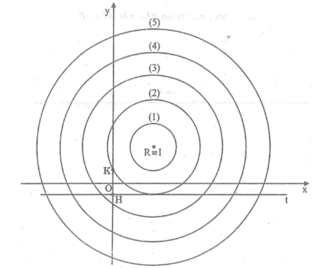
- Đặt tờ giấy kính lên tờ giấy đã vẽ 5 đường tròn sao cho đường tròn (1) đi qua K và tiếp xúc với Ht và tâm I nằm bên phải Oy. Trên tờ giấy kính, đánh dấu vào chỗ điểm I xuất hiện và kí hiệu là điểm A.
- Di chuyển tờ giấy kính sang trái sao cho đường tròn (2) đi qua K và tiếp xúc với Ht. Trên tờ giấy kính, đánh dấu vào chỗ điểm I xuất hiện và kí hiệu là điểm B (xem hình dưới).
- Tiếp tục làm như thế đối với các đường tròn còn lại ta lần lượt được các điểm C, D, E trên tờ giấy kính.
- Lấy các điểm A’, B’, C’, D’, E’ lần lượt đối xứng với các điểm A, B, C, D, E qua Oy.
- Nối các điểm E’, D’, C’, B’, A’, A, B, C, D, E bởi một đường cong ta được một parabol.
Cho hình vuông cạnh bằng a,vẽ vào phía trong hình vuông các cung tròn 900 có tâm lần lượt là các đỉnh của hình vuông,bán kính \(\dfrac{a}{2}\). Hãy cho biết diện tích của phần tạo bởi 4 cung tròn đó và hình vuông
A.a2\(\left(1-\dfrac{\pi}{2}\right)\)) B.a2\(\left(1-\dfrac{\pi}{4}\right)\) C.a2\(\left(1-\pi\right)\) D.a2-\(\dfrac{\pi}{4}\)
Cho hình vuông ABCD có độ dài cạnh là 1 dm. Vẽ hai đường tròn có bán kính bằng cạnh của hình vuông có tâm lần lượt là A và C. Hãy tính diện tích của phần gạch chéo trong hình.