Cho đường tròn (O), đường kính AB. Kẻ hai dây song son AC và BD. Chứng minh rằng:
a) AC = BD;
b) Ba điểm C, O, D thẳng hàng.
Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. Chứng minh AC = BD
Đường thẳng qua O và vuông góc với AC và BD lần lượt tại H và K (H ∈ AC; KBD)
Ta có ∆AOH = ∆BOK (g.c.g) => AK = BK => AC = BD
Cho đường tròn (O) đường kính AB. Kẻ 2 dây AC bà BD song song. Chứng minh: AC=BD
Ta có :
AC // BD
=> \(\begin{cases}\widehat{A_2}=\widehat{B_2}\\\widehat{C_2}=\widehat{D_2}\end{cases}\)
Từ giác ABCD nội tiếp đường tròn
=> \(\widehat{A_2}=\widehat{C_2}\)
\(\Rightarrow\widehat{A_2}=\widehat{B_2}=\widehat{C_2}=\widehat{D_2}\)
\(\Rightarrow\begin{cases}OA=OC\\OB=OD\end{cases}\)
Tương tự ta có \(\begin{cases}OA=OD\\OB=OC\end{cases}\)
\(\Rightarrow OA=OB=OC=OD\)
\(\Rightarrow AB=CD\)
Cho (O) đường kính AB, kẻ hai dây AC và BD song song với nhau.
a) Chứng minh AC= BD; b) Chứng minh 3 điểm C, O, D thẳng hàng.
Cho đường tròn (O) có AB là đường kính. Vẽ hai dây AD và BC song song nhau. Chứng minh:
a, AC = BD
b, CD là đường kính của (O)
Cho đường tròn tâm O, đường kính AB, vẽ hai dây AB CD song song nhau. kẽ OI vuông góc AC a) Chứng minh OI vuông góc BD tại K. b ) Chứng minh tam giác IOA = tam giác OKB. c) So sánh AC và BD
Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ dây CD song song với AB. Chứng minh rằng BC = BD.
Ta có OB ⊥ AB và AB // CD nên OB ⊥ CD. Gọi H là giao điểm của BO và CD thì BH ⊥ CD, suy ra HC = HD. Do đó BC = BD.
Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ dây CD song song với AB. Chứng minh rằng BC = BD ?
Cho đường tròn (O) đường kính AB. Kẻ hai dây AC và BD song song. Chọn khẳng định đúng trong các khẳng định sau.
A. AC = BD
B.AC = 2 BD
C. BD = 2 AC
D. Tất cả sai
Đáp án A
Qua O dựng đường thẳng vuông góc với AC và BD. Đường thẳng này cắt AC và BD lần lượt tại M và N.
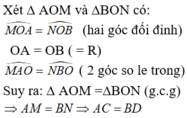
Cho đường tròn tâm O đường kính AB. Từ A và Bvẽ hai dây AC và BD song song với nhau. So sánh hai cung nhỏ A C ⏜ và B D ⏜
Ta chứng minh được ∆ABC = ∆BDA từ đó suy ra A C ⏜ = B D ⏜