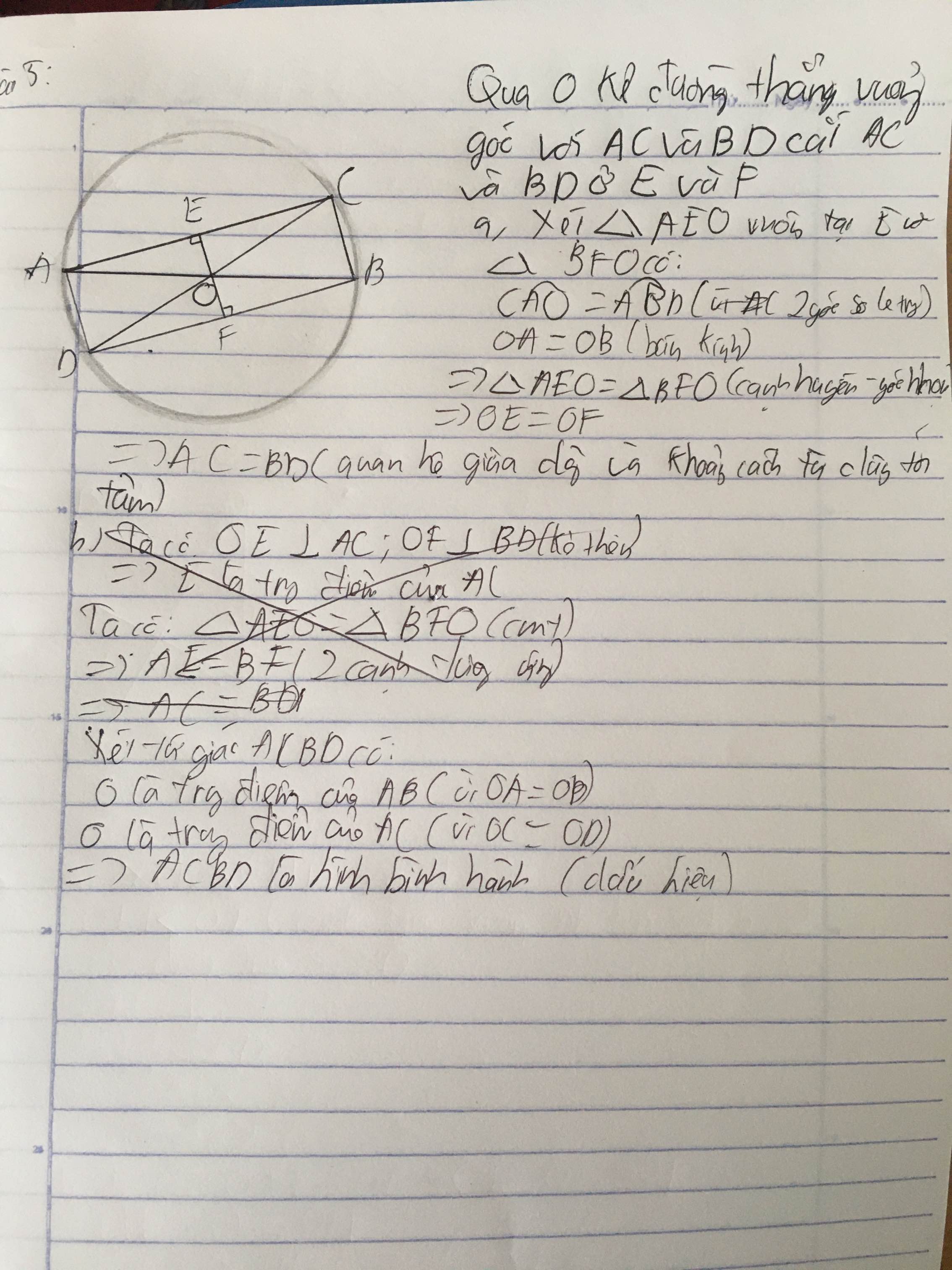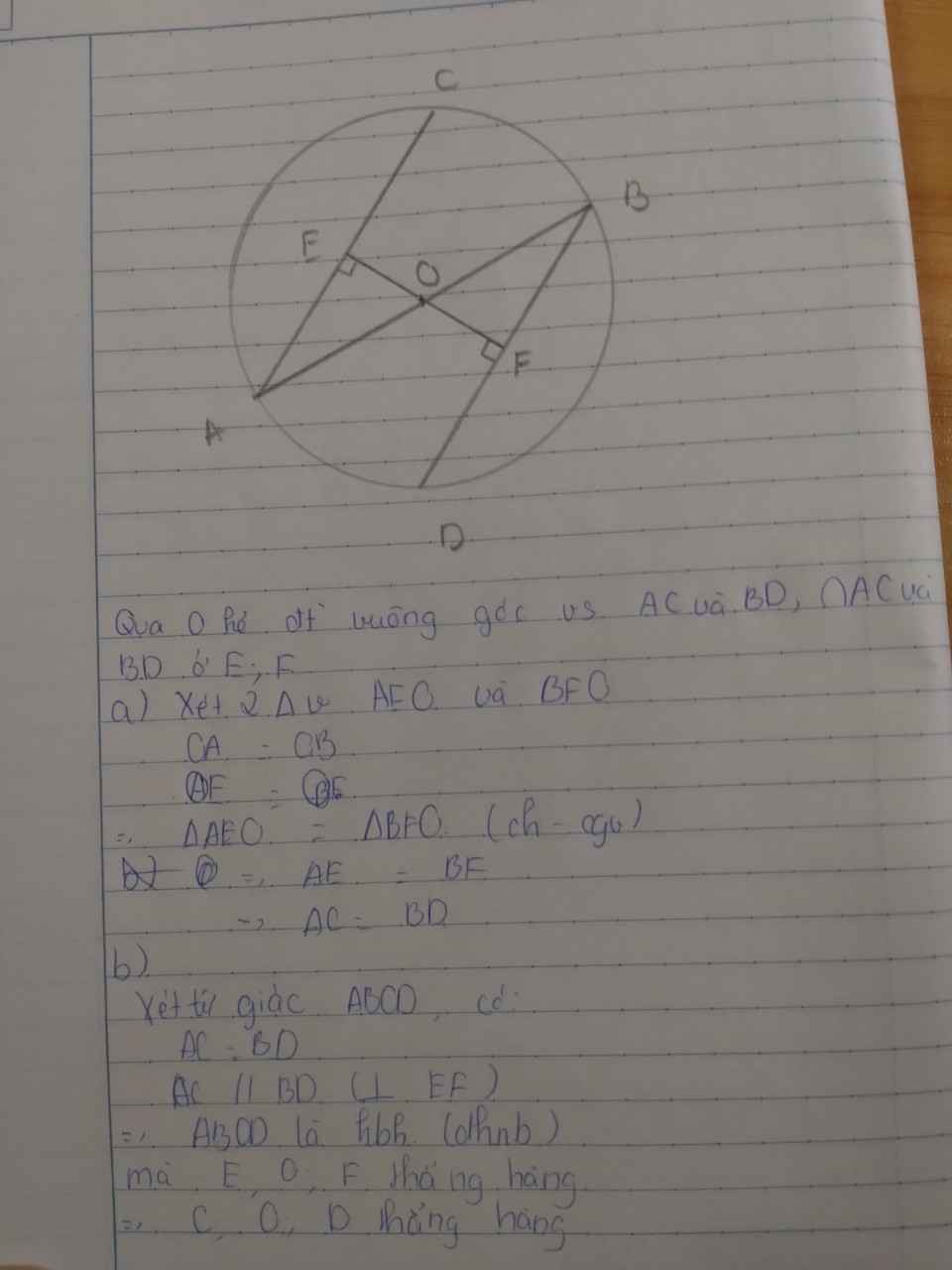a Tg aeo=tg bfo,bABCD la hinh binh hanh
Giải thích các bước giải:
a)Ta có :
Xét tam giác DOB và tam giác AOC , ta có :
(hai gócsole trong mà )
(hai góc đối đỉnh )
(cạnh tương ứng)
b) Ta có :
mà
thẳng hàng
Tam giác AOC và BOD là 2 tam giác cân do OA=OB=OC=OD=bkính
góc CAO = góc DBO ( so le trong )
từ đó suy ra tam giác AOC=tam giác BOD
=> AC=BD suy ra cung AC=cung BD
cung CD=CB+BD=CB+AC=cung AB
suy ra CD là đường kính hay C,O,D thẳng hàng
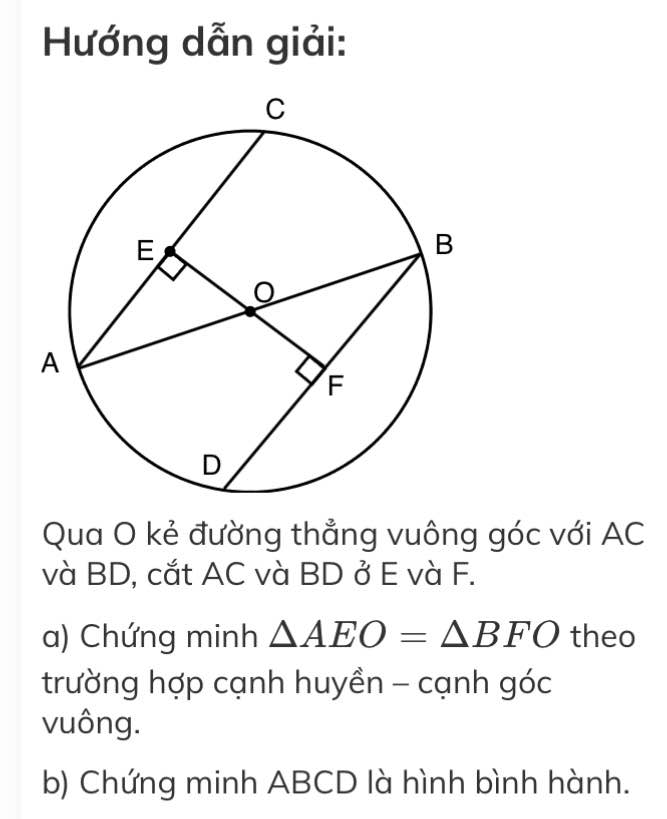
Qua O kẻ đường thẳng vuông góc với AC và BD, cắt AC và BD ở E và F.
a) Chứng minh \Delta AEO=\Delta BFO theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh ABCD là hình bình hành.
Qua O kẻ đường thẳng vuông góc với AC và BD , cắt AC và BD ở E và F.
a)Xét ΔAEO và Δ BFO có:
OA=OB (=R)
Góc EAO = góc OBF( so le trong)
Vậy ΔAEO=ΔBFO
⇒OF=OE
⇒AC=BD
b)Vì AO=OB
⇒OD=OC
⇒ACBD là hình bình hành
⇒C,D,O thẳng hàng
a)Qua O kẻ đường thẳng vuông góc với AC và BD, cắt AC và BD ở E và F.(1)
Xét 2 tam giác vuông OEA và OFB có
góc EAO=góc OBF(sole trong)
OA=OB(bán kính)
=>ΔAEO=ΔBFO(cạnh huyền -góc nhọn) (2)
=>OE=OF
=>AC=BD(liên hệ giữa dây và khoảng cách từ dây tới tâm)
b) Từ (1)=>E,F lần lượt là trung điểm của AC,BD
(2)=>AE=BF
=>AC=BD mà AC song song vs BD=>ACBD là hbh
a,Kẻ OE vuông góc với Ab và OH vuông góc với CD
Xét △ AEO vuông tại E và△BOH vuông tại H có :
OA=OB ( bán kính )
Góc EOA = Góc BOH( đối đỉnh )
⇒△ AEO=△BHO ( cạnh huyền - góc nhọn )
⇒OE=OF ( 2 cạnh tương ứng )
⇒AB=CD ( liên hệ giữa khoảng cách từ tâm đến dây )
b,XÉt tứ giác ADBC có O là trung điểm của AB và O cũng là trung điểm của CD
⇒tứ giác ADBC là hình bình hành ( dhnb)
⇒ C , O , D thẳng hàng ( đpcm )
a)Tam giác AEO=Tam giác BFO(cạnh huyền-cạnh góc vuông)
b) Tứ giác ABCD hình bình hành;O là giao điểm của hai đường chéo AB và CD
Qua O kẻ đường thẳng vuông góc với AC và BD, cắt AC và BD ở E và F.
a) Chứng minh theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh ABCD là hình bình hành.
a,AC=BD
b,O,D,C Thẳng hàng
Qua O kẻ đường thẳng vuông góc với AC và BD, cắt AC và BD ở E và F.
a) Chứng minh theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh ABCD là hình bình hành.
a) Chứng minh theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh ABCD là hình bình hành.
Qua O kẻ đường thẳng vuông góc với AC và BD, cắt AC và BD ở E và F.
a) Chứng minh theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh ABCD là hình bình hành.
a,O kẻ đường thẳng vuông góc với AC và BD, cắt AC và BD ở E và F.
Xét Δ AEO và ΔBFO có : AO=BO (=R) ;góc EOA = góc BOF ( 2 góc đối đỉnh); góc AEO= góc BFO =90 độ (OE vuông góc với AC , OFvuông góc với BD) Vậy Δvg AEO=ΔvgBFO ( cạnh huyền góc nhọn) => AE=BF (2 cạnh tương ứng)=>AC=BD(quan hệ vuông góc giữa đường kính và dây ) b, tứ giác ACBD có AC=BD và AC//BD => ACBD là hbh ( theo dhnb của hbh) => Hai đường chéo AB và CD bằng nhau cắt nhau tại trung điểm của mỗi đường => O là trung điểm của CD và CD cũng là đường kính => Ba điểm O,C,D thẳng hàng.
Kẻ OE vuông góc với AC tại E ⇒OE vuông góc với BD tại F
2△vuông EOA và FOB có:
OA =OB (bán kính)
góc A =góc B ( so le trong)
nên △EOA = △FOB ⇒EA=FB
Ta có :EA=EC=\(\dfrac{1}{2}\)AC
FD=FB=\(\dfrac{1}{2}\)DB
Do đó:AC = DB
Qua O kẻ đường thẳng vuông góc với AC và BD ,cắt AC và BD ở E và F
a, xét ΔOAE và ΔOBF có:
OA \(=\)OB
ΔOAE \(=\)ΔOBF(cạnh huyền-góc vuông)
\(\Rightarrow\)AC \(=\)DB ( 2 cạnh tương ứng)
b, Xét tứ giác ABCD có; AC\(=\)DB(CMT), AC//DB(GT)
\(\Rightarrow\)Tứ giác ABCD là hình bình hành(dhnb)
Mà CD và AB lại là hai đường chéo của tứ giác ABCD cắt nhau tại O
\(\Rightarrow\) C,O,D thẳng hàng
Qua O kẻ đường thẳng vuông góc với AC và BD, cắt AC và BD ở E và F.
a) Chứng minh theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh ABCD là hình bình hành.
Qua O kẻ đường thẳng vuông góc với AC tại E và BD tại F
a) Xét hai tam giác vuông OEA và OFB
OA =OB ( AB là đường kính )
OE =OF
=> tam giác AEO bằng tam giác BFO ( cạnh huyền - cạnh góc vuông )
=> AE bằng BF hay AC = BD
b) Xét tứ giác ACBD có
AC//BD ( gt)
AC=BD ( cmt)
=> tứ giác ACBD là hình bình hành ( dhnb )
C , O ,D thẳng hàng
Qua O kẻ đường thẳng vuông góc với AC và BD, cắt AC và BD ở E và F.
a) Chứng minh theo trường hợp cạnh huyền – cạnh góc vuông.
b) Chứng minh ABCD là hình bình hàn
qua O kẻ đường thẳng vuông góc với AC và BD , cắt AC và BD ở E và F (1)
xét hai tam giác vuông OEA và OFB
góc EAO= góc OBF(so le trong)
OA=OB(bán kính)
=>tam giác OEA=tam giác OFB
a, qua o kẻ đường thẳng vuông góc với ACvà BD cắt AC và BD ở E và F (1)
xét ΔOEA và ΔOFB có
góc EAO = góc OBE (hai góc so le trong bằng nhau)
OA=OB( bán kính)
⇒ΔAEO = ΔBFI ( cạnh huyền -góc nhọn )( 2)
⇒OE = OF
⇒AC = BD(l liên hệ giữa đây và khoảng cách từ dây tới tâm)
b,từ (1) ⇒ E,F lần lượt là trung điểm AC,BD
Tứ( 2)⇒AE=BF
⇒AC=BD mà AC// BD
⇒ACBD là hình bình hành
a) chứng minh tam giác AEO= tam giác BFO
b)chứng minh ABCD là hình bình hành