***CHO hình vuông ABCD . Vẽ AH vuông góc với BD. Gọi P; Q lần lượt là trung điểm của BH; DC.
CMR: PQ vuông góc với AP
Những câu hỏi liên quan
Cho hình bình hành ABCD (AB > BC), gọi M và N lần lượt là trung điểm của AB và CD.
a) Chứng minh AN//MC
b) Từ A vẽ AH vuông góc với BD (H thuộc BD), từ C vẽ CK vuông góc với BD (K thuộc BD). Tứ giác AHCK là hình gì? Vì sao?
c) AH cắt CD tại E, CK cắt AB tại F. Gọi O là trung điểm của HK. Chứng minh E, O, F thẳng hàng
giúp em với ạ em đang cần gấp :<<
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra:AN//CM
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có góc A=góc B=90o và AD=2BC. Kẻ AH vuông góc với BD (H thuộc BD). Gọi I là trung điểm của HD. CMR CI vuông góc với AI
bài 1) Cho hình bình hành ABCD,vẽ AH vuông góc với DB tại H ,vẽ HC vuông góc với BD tại K(vẽ hình trước khi làm)a)cm:AHCK là hình bình hànhb)cm: Δ DHC Δ BKAc) Gọi I là trung điểm của HK ; cm:I là trung điểm DB theo tính chất của hình bình hành
Đọc tiếp
bài 1) Cho hình bình hành ABCD,vẽ AH vuông góc với DB tại H ,vẽ HC vuông góc với BD tại K(vẽ hình trước khi làm)a)cm:AHCK là hình bình hànhb)cm: Δ DHC= Δ BKAc) Gọi I là trung điểm của HK ; cm:I là trung điểm DB theo tính chất của hình bình hành
Cho hình thang vuông ABCD có góc A=góc B=90o và AD=2BC. kẻ AH vuông góc với BD. Gọi I là trung điểm của HD. cmr CI vuông góc với AI
cho hình thoi ABCD, có AC=6cm và BD=8cm. Vẽ đường AH vuông góc với BC. tính AH ?
bạn sai roi phai ap dung dinh ly ty-ta-go
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Gọi là góc giữa BD và (SAD). Tính sin
α
A. sin
α
6
4
B. sin
α
1
2
C. sin
α
3
2
D. sin
α
...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Gọi là góc giữa BD và (SAD). Tính sin α
A. sin α = 6 4
B. sin α = 1 2
C. sin α = 3 2
D. sin α = 10 4
Đáp án A
Gọi N là trung điểm AD suy ra HN // BD.
Góc giữa BD và (SAD) bằng góc giữa HN và (SAD).
Ta có AD⊥SH, AD⊥AB suy ra AD⊥ (SAB) . Trong mặt phẳng (SAB) kẻ HK⊥SA nên ta suy ra AD⊥HK và HK⊥ (SAD) . vậy góc giữa HN và (SAD) là góc HNK.
Gọi cạnh của hình vuông là a
Ta tính được HN = a 2 2 . Xét tam giác vuông SHA vuông tại H ta có
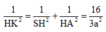
Xét tam giác vuông HNK vuông tại K ta có 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Gọi
α
là góc giữa BD và (SAD). Tính sin
α
A.
sin
α
6
4
B.
sin
α
1
2
C.
sin
α
3
2
D. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Gọi α là góc giữa BD và (SAD). Tính sin α
A. sin α = 6 4
B. sin α = 1 2
C. sin α = 3 2
D. sin α = 10 4
cho hình thang cân ABCD (AB//CD) , vẽ AH của hình thang cân = 10cm. gọi M, N lần lượt là trung điểm của AD và BC. tính dộ đai MN biết AC vuông góc với BD.