a: ΔABC cân tại A

mà AI là phân giác

nên AI vuông góc BC

b: Xét ΔABC có

AI,CM là trung tuyến

AI cắt CM tại G

=>G là trọng tâm

=>BG là đường trung tuyến của ΔABC

các bạn giúp  mik bài này 

a) Xét 2 tam giác BAI và tam giác CAI, ta có:

       AB = AC (giả thiết tam giác cân)

 góc BAI = góc CAI (AI là tia phân giác góc A)

       AI là cạnh chung

\(\Rightarrow\Delta\) BAI = \(\Delta\) CAI (c.g.c)

\(\Rightarrow\) góc BIA = góc CIA (hai góc tương ứng)

Mà 2 góc này ở vị trí kề bù nên ta có: góc BIA = góc CIA = 1/2.\(180^0\)=\(90^0\)

\(\Rightarrow\) AI vuông góc với BC

b) Ta có: BI = CI (2 cạnh tương ứng do tg BAI = tg CAI)

\(\Rightarrow\) AI là trung tuyến của tg ABC

Lại có: BD là trung tuyến của tg ABC

Mà AD giao với BC tại M nên M là trọng tâm của tg ABC

c) Ta có: BI = CI = 1/2.BC = 1/2.6 = 3(cm)

 Áp dụng định lí Pitago vào tg vuông AIB có:

            \(AB^2=BI^2+AI^2\)

            \(\Rightarrow AI^2=AB^2-BI^2\)

             \(\Rightarrow AI^2=5^2-3^2=25-9=16\)

            \(\Rightarrow\) \(AI=4\) (cm)

            \(\Rightarrow AM=\frac{2}{3}.AI=\frac{2}{3}.4=\frac{8}{3}\) (cm)

Vậy AM = 8/3 (cm)

Chúc bạn học tốt !!!

Có ai vẽ hik giùm mik đc ko

a,Ta có:AD vuông góc với BC(gt)

            BE vuông góc với AD(gt)

Mà AD cắt BE tại H (gt)

Từ đó suy ra H là trực tâm

Mà H thuộc CH,suy ra CH vuông góc AB

câu b khó ghê, cm vuông góc mk k giải dc, 

Bạn tự vẽ hình nhé

a) Gọi D là giao điểm của BI với AC; M là giao điểm của BG với AC.

Trong tg ABC có BD là phân giác => \(\frac{BC}{DC}=\frac{AB}{DA}=\frac{BC+AB}{DC+DA}=\frac{8}{AB}=\frac{8}{4}=2\)2

Trong tam giác BCD có CI là phân giác => \(\frac{IB}{ID}=\frac{BC}{DC}=2\)

Mặt khác do G là trọng tâm nên có \(\frac{BG}{GM}=2\)

Vậy suy ra \(\frac{IB}{ID}=\frac{BG}{GM}\)do đó IG //AC (Talet đảo)

b) Từ câu a) bạn tự tính IG nhé

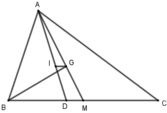
Gọi D, M là giao điểm của AI, AG với BC.

Vì AD là tia phân giác góc B A C ^  nên B D A B = D C A C  (t/c)

⇒ B D 12 = D C 18 = B D + D C 12 + 18 = 15 30 = 1 2

=> BD = 12. 1 2  = 6, DC =18. 1 2  = 9

Lại có: BI là tia phân giác A B D ^ nên A I I D = A B B D = 12 6 = 2  (tính chất)

=> I D A D = M G M A = 1 3  hay D đúng

Mà AG = 2GM (vì G là trọng tâm)

Nên A I I D = A G G M = 2  hay B đúng

Theo định lí đảo của định lí Talet ta có:

IG // DM => IG // BC hay A đúng

Chỉ có C sai

Đáp án: C