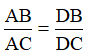trong tam giác đều Em có nhận xét về đường cao đường trung tuyến đường phân giác đường trung trực

Những câu hỏi liên quan
Nhận xét Trong một tam giác, nếu hai trong bốn loại đường ( đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của cạnh này ) trùng nhau thì tam giác đó là một tam giác cân.Từ nhận xét trên hãy chứng minh: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân ai nhank mk tick cho help me tói 9h tối nay phải có nha mk gấp lắm
Đọc tiếp
Nhận xét
Trong một tam giác, nếu hai trong bốn loại đường ( đường trung tuyến, đường phân giác, đường cao cùng xuất phát từ một đỉnh và đường trung trực ứng với cạnh đối diện của cạnh này ) trùng nhau thì tam giác đó là một tam giác cân.
Từ nhận xét trên hãy chứng minh: "Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân "
ai nhank mk tick cho help me tói 9h tối nay phải có nha mk gấp lắm
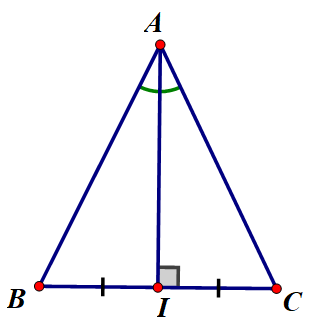
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)
Đúng 0
Bình luận (0)
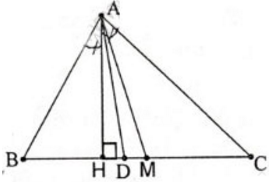
Cho tam giác ABC ( AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.
- Nhận xét: D luôn nằm giữa H và M.
- Chứng minh:

Đúng 0
Bình luận (0)
1.1. Vẽ đường trung tuyến, đường phân giác, đường trung trực, đường cao cùng
xuất phát từ một đỉnh của một tam giác bất kì.
1.2. Vẽ đường trung tuyến, đường phân giác, đường trung trực, đường cao cùng
xuất phát từ một đỉnh của một tam giác cân.
Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M ?
- Nhận xét: D luôn nằm giữa H và M.
- Chứng minh:
Đúng 0
Bình luận (0)
Δ AMB và Δ AMC có: AM chung MB =MC và AC > AB
=> AMC^ > AMB^ => M thuộc CH.(M ở giữa C và H)
AB<AC => B^ > C^ => BAH^ < CAH^ => D thuộc CH.(1)
theo tính chất phân giác:
BD/AB = CD/AC
mà: AC > AB => CD > BD => D thuộc BM (2)
(1) và (2) => D thuộc HM hay D là điểm nằm giữa H và M.
Đúng 0
Bình luận (0)
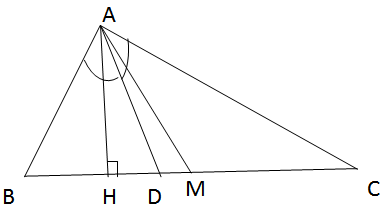
+Nhận xét: D luôn nằm giữa H và M.
+Chứng minh: AD là đường phân giác của ∆ABC.
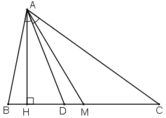
=>ABAC=DBDCABAC=DBDC AB < AC
=>DB < DC => DB + DC < DC + DC
=>BD + DC < 2DC hay BC < 2DC => DC >BC2BC2
Mà MC=BC2MC=BC2 (M là trung điểm của BC)
=>DC > MC =>M nằm giữa D và C (1)
+Mặt khác: ˆCAH=900–^CCAH^=900–C^ (∆CAH vuông tại H)
^A+^B+^C=1800A^+B^+C^=1800 (tổng 3 góc ∆ABC)
=>ˆCAH=^A+^B+^C2–^CCAH^=A^+B^+C^2–C^
=>ˆCAH=^A2+^B2–^C2=^A2+^B–^C2CAH^=A^2+B^2–C^2=A^2+B^–C^2
Vì AB < AC =>ˆC<ˆB⇒ˆB–ˆC>0C^<B^⇒B^–C^>0
Do đó: ˆCAH>^A2CAH^>A^2 hay ˆCAH>ˆCADCAH^>CAD^
=>Tia AD nằm giữa hai tia AH và AC =>D nằm giữa hai điểm H và C (2)
Từ (1) và (2) => D nằm giữa H và M.
Đúng 0
Bình luận (0)
Những tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao?
Tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao là tam giác cân, tam giác vuông cân, tam giác đều.
Đúng 0
Bình luận (0)
Những tam giác nào có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao ?
Tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao là tam giác cân, tam giác vuông cân.
Đúng 0
Bình luận (0)
Trả lời
Tam giác có ít nhất một đường trung tuyến đồng thời là đường phân giác, đường trung trực, đường cao là tam giác cân, tam giác vuông cân.
Đúng 0
Bình luận (0)
Trong một tam giác, điểm cách đều ba cạnh của tam giác là:
a)Giao điểm ba đường trung tuyến
b)Giao điểm ba đường trung trực
c)Giao điểm ba đường phân giác
d)Giao điểm ba đường cao
c, giao điểm 2 đường phân giác
chúc bn hok tốt!
đúng thì k cho mk nha!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Hãy chứng minh nếu tam giác ABC đều thì 3 đường trung tuyến, phân giác, trung trực, đường cao của tam giác đó cùng đồng quy (giao nhau) tại 1 điểm
Cả trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và điểm cách đều 3 cạnh đều là 1 điểm trong tam giác
=>3 đường trung tuyến, phân giác, trung trực, đường cao của tam giác đó cùng đồng quy (giao nhau) tại 1 điểm
nêu một số tính chất của đường trung trực, đường trung tuyến, đường cao, đường phân giác của tam giác
+) Tính chất của đường trung trực của tam giác: 3 đường trung trực của tam giác cắt nhau tại 1 điểm; điểm đó cách đều 3 cạnh của tam giác đó.
+) Tính chất đường cao trong tam giác: 3 đường cao trong tam giác cắt nhau tại 1 điểm
+) Tính chất đường phân giác của tam giác: 2 đường phân giác của tam giác cắt nhau tại một điểm; điểm đó cách đều 3 cạnh của tam giác đó.
+) Tính chất đường trung tuyến của tam giác: 3 đường trung tuyền của tam giác cắt nhau tại một điểm; điểm đó cách mỗi đỉnh khoảng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
Chúc bn học tốt!!!!!!
Đúng 0
Bình luận (0)