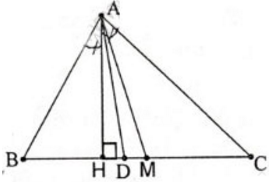
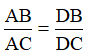- Nhận xét: D luôn nằm giữa H và M.
- Chứng minh:
Δ AMB và Δ AMC có: AM chung MB =MC và AC > AB
=> AMC^ > AMB^ => M thuộc CH.(M ở giữa C và H)
AB<AC => B^ > C^ => BAH^ < CAH^ => D thuộc CH.(1)
theo tính chất phân giác:
BD/AB = CD/AC
mà: AC > AB => CD > BD => D thuộc BM (2)
(1) và (2) => D thuộc HM hay D là điểm nằm giữa H và M.
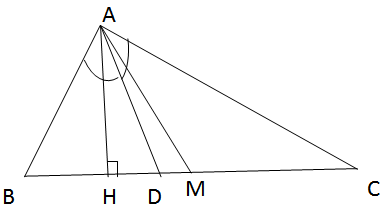
+Nhận xét: D luôn nằm giữa H và M.
+Chứng minh: AD là đường phân giác của ∆ABC.
=>ABAC=DBDCABAC=DBDC AB < AC
=>DB < DC => DB + DC < DC + DC
=>BD + DC < 2DC hay BC < 2DC => DC >BC2BC2
Mà MC=BC2MC=BC2 (M là trung điểm của BC)
=>DC > MC =>M nằm giữa D và C (1)
+Mặt khác: ˆCAH=900–^CCAH^=900–C^ (∆CAH vuông tại H)
^A+^B+^C=1800A^+B^+C^=1800 (tổng 3 góc ∆ABC)
=>ˆCAH=^A+^B+^C2–^CCAH^=A^+B^+C^2–C^
=>ˆCAH=^A2+^B2–^C2=^A2+^B–^C2CAH^=A^2+B^2–C^2=A^2+B^–C^2
Vì AB < AC =>ˆC<ˆB⇒ˆB–ˆC>0C^<B^⇒B^–C^>0
Do đó: ˆCAH>^A2CAH^>A^2 hay ˆCAH>ˆCADCAH^>CAD^
=>Tia AD nằm giữa hai tia AH và AC =>D nằm giữa hai điểm H và C (2)
Từ (1) và (2) => D nằm giữa H và M.