Ôn tập: Tam giác đồng dạng

1. Đoạn thẳng tỉ lệ

- Tỉ số của hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng đó theo cùng một đơn vị đo.

Ví dụ: \(AB=a\left(cm\right),CD=b\left(cm\right)\) thì \(\dfrac{AB}{CD}=\dfrac{a}{b}\)

- Hai đoạn thẳng \(AB\) và \(CD\) được gọi là tỉ lệ với hai đoạn thẳng \(A'B'\) và \(C'D'\) nếu có tỉ lệ thức:

           \(\dfrac{AB}{CD}=\dfrac{A'B'}{C'D'}\) hay \(\dfrac{AB}{A'B'}=\dfrac{CD}{C'D'}\)

Ví dụ: \(AB=2m\), \(CD=5m\), \(A'B'=10m\), \(C'D'=25m\) thì \(\dfrac{AB}{CD}=\dfrac{A'B'}{C'D'}=\dfrac{2}{5}\)

 Ta nói rằng hai đoạn thẳng \(AB\) và \(CD\) tỉ lệ với hai đoạn thẳng \(A'B'\) và \(C'D'\).

2. Định lí Ta-lét và hệ quả

- Định lí Ta-lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

Ví dụ: Nếu \(\Delta ABC\) có \(B'C'\)//\(BC\) (\(B'\in AB,C'\in AC\))

         Thì ta có: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\), \(\dfrac{B'B}{AB}=\dfrac{C'C}{AC}\) , \(\dfrac{AB'}{B'B}=\dfrac{AC'}{C'C}\).

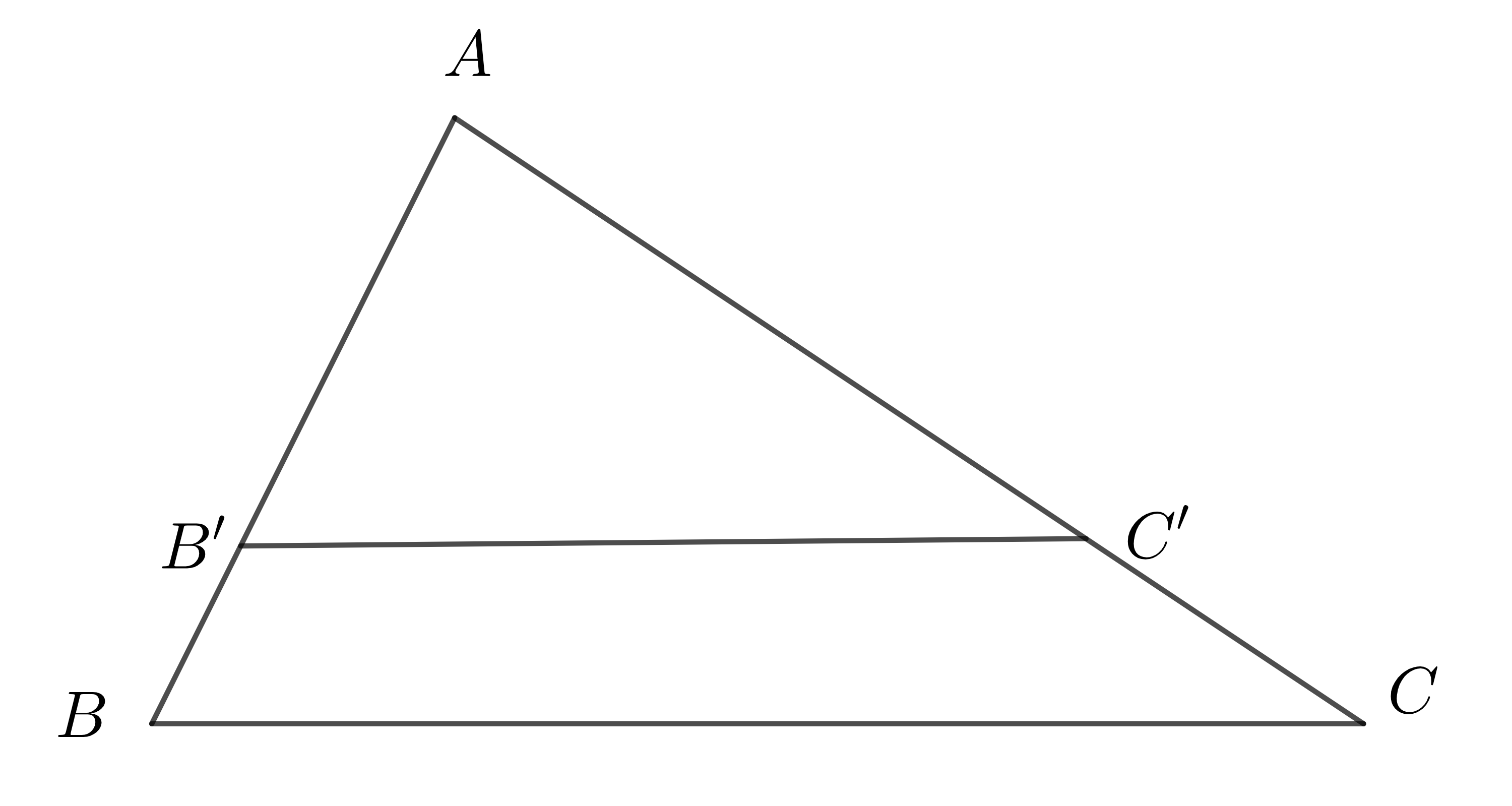
- Định lí Ta-lét đảo: Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Ví dụ: Nếu \(\Delta ABC\) có \(B'\in AB,C'\in AC\) sao cho \(\dfrac{AB'}{B'B}=\dfrac{AC'}{C'C}\)

          Thì \(B'C'\)//\(BC\).

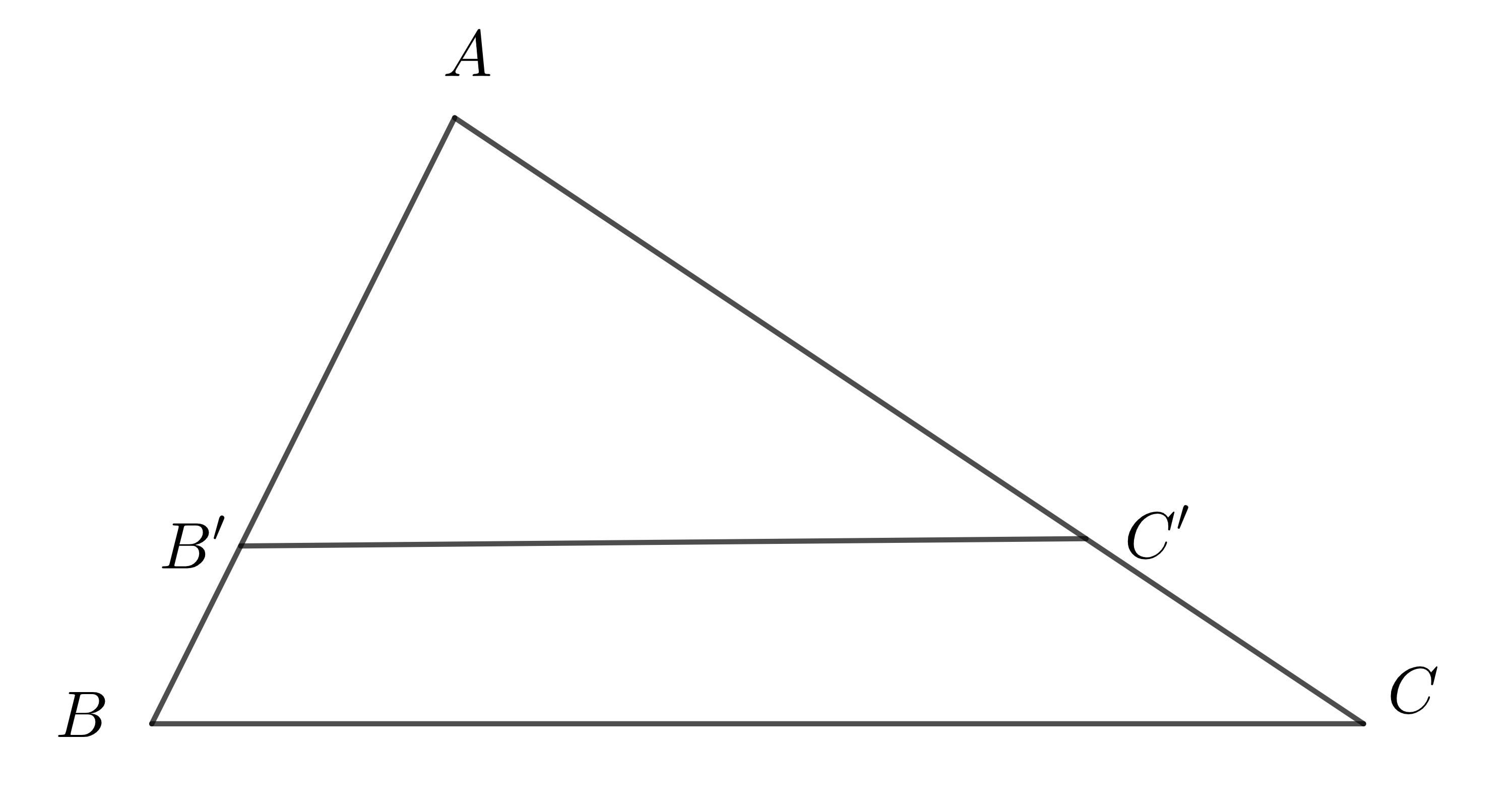
- Hệ quả của định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Ví dụ: Nếu \(\Delta ABC\) có \(B'C'\)//\(BC\) (\(B'\in AB,C'\in AC\))

           thì \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}=\dfrac{B'C'}{BC}\).

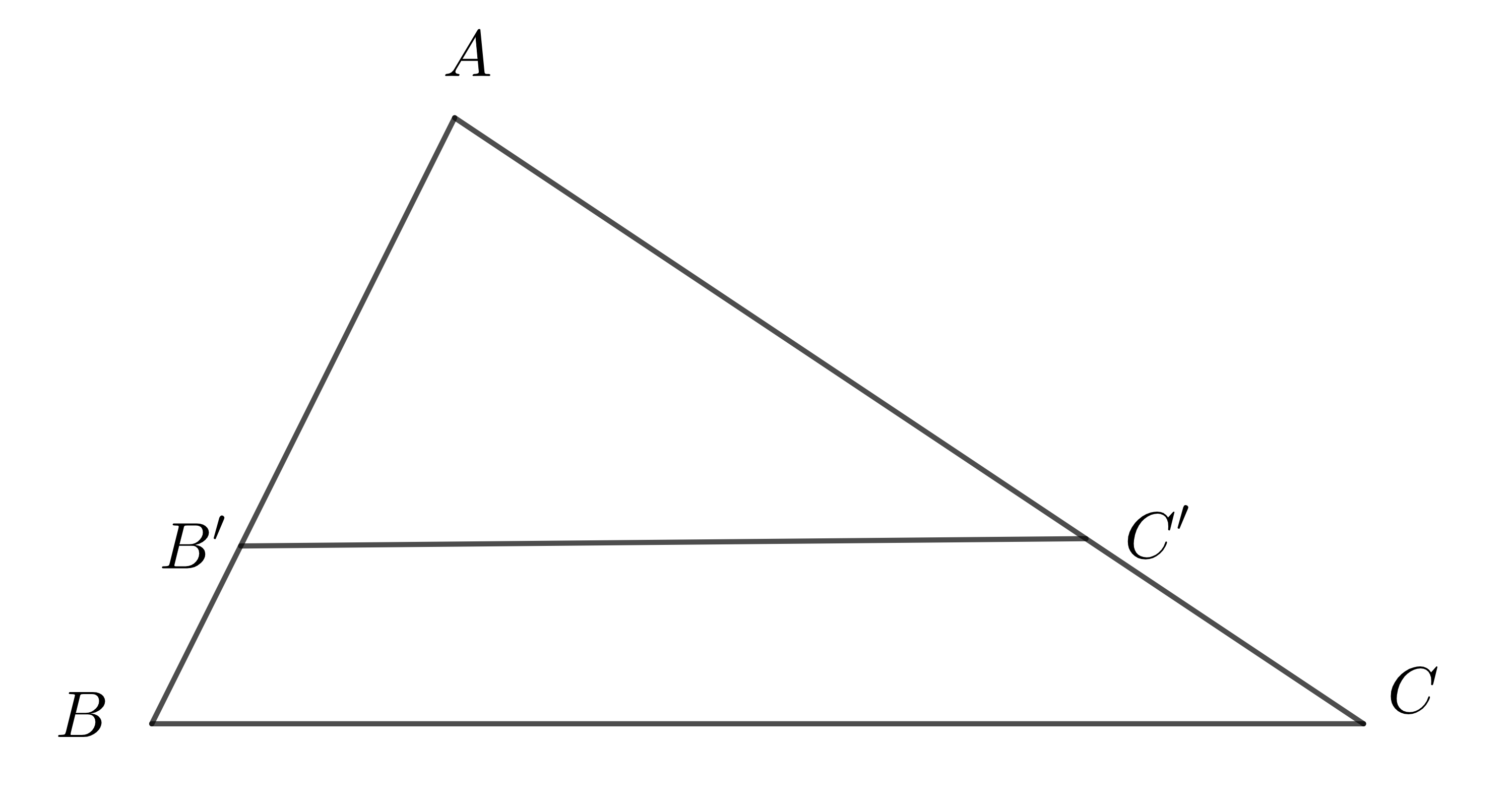
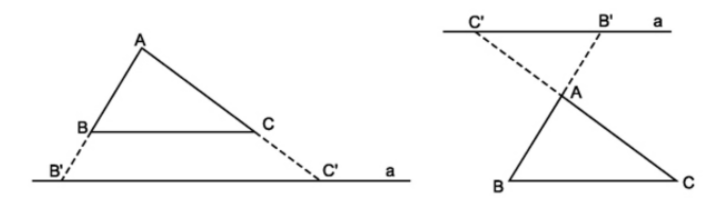
- Hệ quả trên vẫn đúng trong trường hợp đường thẳng \(a\) song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.

3. Tính chất đường phân giác của tam giác

- Định lí: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.

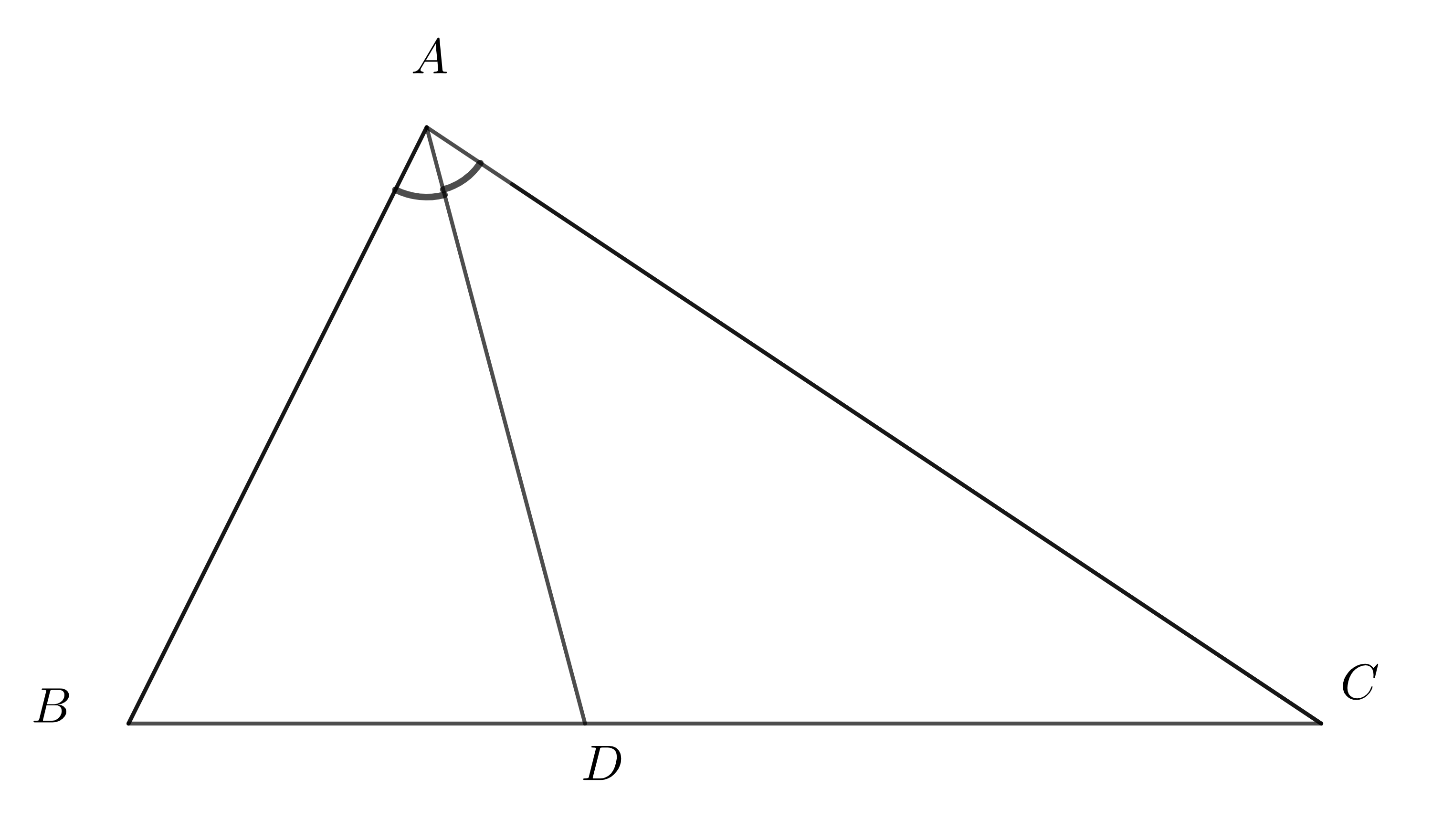
Ví dụ: \(\Delta ABC\) có \(AD\) là phân giác góc \(\widehat{A}\) (\(D\in BC\))

          Thì ta có: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\) hay \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

- Chú ý: Định lí vẫn đúng đối với tia phân giác của góc ngoài của tam giác.

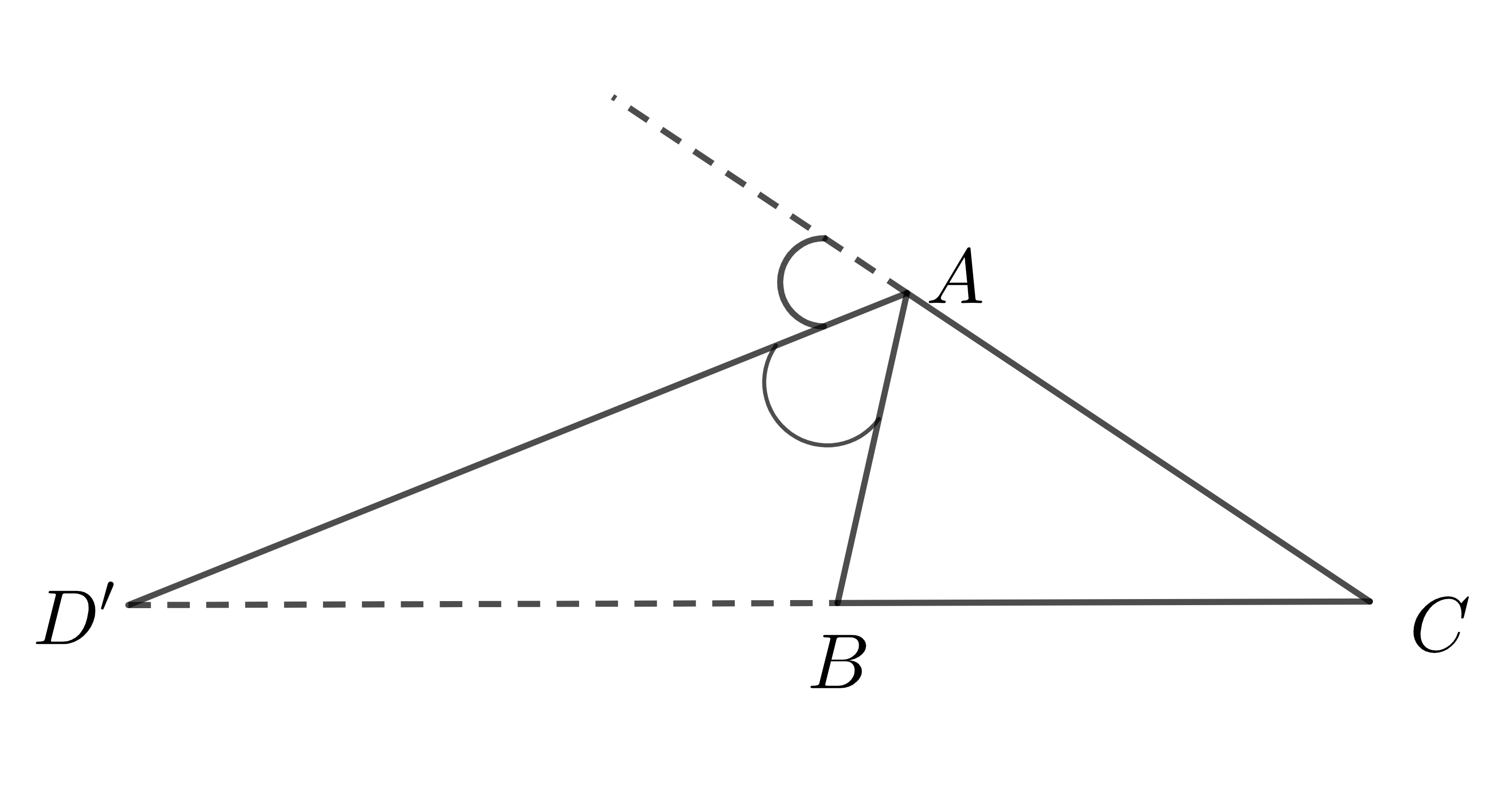
Ví dụ: \(\Delta ABC\) có \(AD'\) là phân giác góc ngoài của góc \(\widehat{A}\) (\(D'\in BC\))

          Thì ta có: \(\dfrac{D'B}{D'C}=\dfrac{AB}{AC}\)

4. Tam giác đồng dạng

- Định nghĩa: Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu:

                      \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}\)

- Tỉ số các cạnh tương ứng \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}=k\)  được gọi là tỉ số đồng dạng.

- Tính chất:

+ Tính chất 1: Mỗi tam giác đồng dạng với chính nó.

+ Tính chất 2: Nếu \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k\) thì \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{1}{k}\).

+ Tính chất 3: Nếu \(\Delta A'B'C'\) đồng dạng với \(\Delta A"B"C"\) theo tỉ số \(k_1\) và \(\Delta A"B"C"\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k_2\) thì \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) theo tỉ số \(k_1.k_2\)

+ Tính chất 4: Tỉ số chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng;

                       Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng;

                       Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.

- Định lí: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại của tam giác thì nó tại thành một tam giác mới đồng dạng với tam giác đã cho.

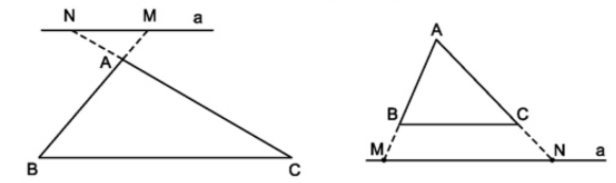
Ví dụ: \(\Delta ABC\) có \(M\in AB,N\in AC\) sao cho \(MN\)//\(BC\)

           Thì \(\Delta AMN\) đồng dạng với \(\Delta ABC\).

- Chú ý: Định lí trên cũng đúng đối với trường hợp đường thẳng \(a\) cắt phần kéo dài hai cạnh của tam giác và song song với cạnh còn lại.

5. Các trường hợp đồng dạng của tam giác:

- Trường hợp đồng dạng thứ nhất: Nếu ba cạnh của tam giác này đồng dạng với một canh của tam giác kia thì hai tam giác đó đồng dạng.

Ví dụ: Nếu \(\Delta ABC\) và \(\Delta A'B'C'\) có \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{C'A'}{CA}\) 

          Thì \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\).

- Trường hợp đồng dạng thứ hai: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cạnh ấy bằng nhau thì hai tam giác đó đồng dạng với nhau.

Ví dụ: Nếu \(\Delta A'B'C'\) và \(\Delta ABC\) có: \(\widehat{A'}=\widehat{A}\) và \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}\)

           Thì \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\).

- Trường hợp đồng dạng thứ ba: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

Ví dụ : Nếu \(\Delta A'B'C'\) và \(\Delta ABC\) có \(\widehat{A'}=\widehat{A}\) và \(\widehat{B'}=\widehat{B}\) 

           Thì \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\).

6. Các trường hợp đồng dạng của tam giác vuông

- Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

Ví dụ: Nếu \(\Delta ABC\) vuông tại \(A\) và \(\Delta DEF\) vuông tại \(D\) có \(\widehat{B}=\widehat{E}\)

          Thì \(\Delta ABC\) đồng dạng với \(\Delta DEF\)

- Nếu tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

Ví dụ: Nếu \(\Delta ABC\) vuông tại \(A\) và \(\Delta DEF\) vuông tại \(D\) có \(\dfrac{AB}{DE}=\dfrac{AC}{DF}\)

          Thì \(\Delta ABC\) đồng dạng với \(\Delta DEF\)

- Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

Ví dụ: Nếu \(\Delta ABC\) vuông tại \(A\) và \(\Delta DEF\) vuông tại \(D\) có \(\dfrac{AB}{BC}=\dfrac{DE}{EF}\)

          Thì \(\Delta ABC\) đồng dạng với \(\Delta DEF\)

7. Ứng dụng thực tế của tam giác đồng dạng

Người ta có thể sử dụng tam giác đồng dạng vào một số tình huống trong thực tế như:

- Đo gián tiếp chiều cao của một vật 

- Đo khoảng cách giữa hai địa điểm trong đó một địa điểm không thể tới được.

Dụng cụ thường sử dụng để đo độ lớn của một góc là giác kế. Giác kế gồm 2 loại:

- Giác kế ngang

- Giác kế đứng