hỏi có bao nhiêu điểm trên hình tứ diện và cả bên trong tứ diện
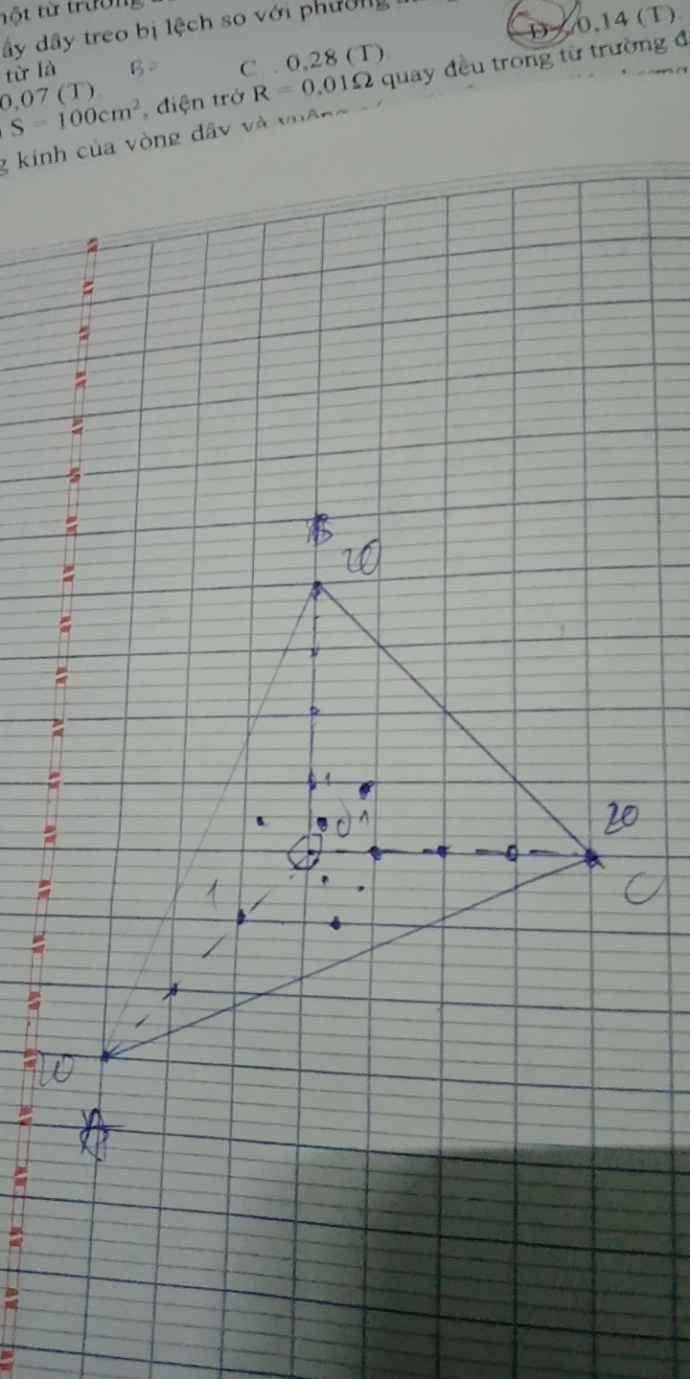
Cho tứ diện ABCD và một điểm G nằm bên trong khối tứ diện như hình vẽ bên. Khẳng định nào dưới đây là đúng về cách
phân chia khối tứ diện trên?
A. Khối tứ diện ABCD được phân chia thành 2 khối là B.AGC và D.AGC
B. Khối tứ diện ABCD được phân chia thành 3 khối là G.ABD; G.ABC; G.ACD
C. Khối tứ diện ABCD được phân chia thành 3 khối là G.BCD; G.ABC; G.ACD
D. Khối tứ diện ABCD được phân chia thành 4 khối là A.DGB; G.ABC; A.GCD; G.BCD
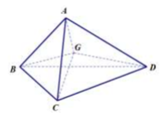
Cho tứ diện ABCD và một điểm G nằm bên trong khối tứ diện như hình vẽ bên. Khẳng định nào dưới đây là đúng về cách phân chia khối tứ diện trên?
A. Khối tứ diện ABCD được phân chia thành 2 khối là B.AGC và D.AGC
B. Khối tứ diện ABCD được phân chia thành 3 khối là G.ABD; G.ABC; G.ACD
C. Khối tứ diện ABCD được phân chia thành 3 khối là G.BCD; G.ABC; G.ACD
D. Khối tứ diện ABCD được phân chia thành 4 khối là A.DGB; G.ABC; A.GCD; G.BCD
Trong Oxyz cho A 3 ; 0 ; 0 , B 3 ; 2 ; 0 , C 0 ; 2 ; 0 và O ' 0 ; 0 ; 1 . Xét hình hộp chữ nhật OABCO'B'C'D'. Hỏi có bao nhiêu tứ diện mà có 4 đỉnh đều là đỉnh hình hộp chữ nhật trên mà thể tích của tứ diện đó bằng 2?
![]()
![]()
![]()
![]()
Cho một tam giác ABC vuông cân có AB = AC = 12cm. Điểm M chạy trên AB. Tứ giác MNCP là một hình bình hành có đỉnh N thuộc cạnh AC (hình bên). Hỏi khi M cách A bao nhiêu thì diện tích của hình bình hành bằng 32 c m 2 ?
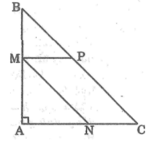
Gọi x (cm) là độ dài đoạn AM.
Điều kiện: 0 < x < 12
Vì ΔABC vuông cân tại A nên ΔBMP vuông cân tại M.
Suy ra MP = MB = AB – AM = 12 – x (cm)
Diện tích hình bình hành MNCP bằng MP.MA = (12 – x)x ( c m 2 )
Theo đề bài, ta có phương trình:
(12 – x)x = 32 ⇔ x 2 – 12x + 32 = 0
∆ ' = - 6 2 – 1.32 = 36 – 32 = 4 > 0
∆ ' = 4 = 2
![]()
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán
Vậy điểm M cách điểm A 8cm hoặc 4cm thì diện tích hình bình hành MNCP bằng 32 c m 2
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A 0 ; 0 ; 3 , B 0 ; 3 ; 0 , C 3 ; 0 ; 0 , D 3 ; 3 ; 3 . Hỏi có bao nhiêu điểm M x ; y ; z (với x, y, z nguyên) nằm trong tứ diện.
A. 4
B. 1
C. 10
D. 7
Đáp án A.
Cách 1:

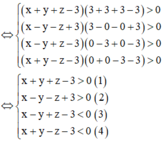
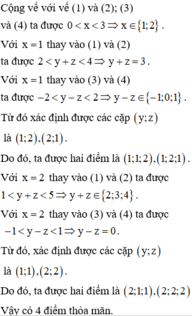

Do các mặt của tứ diện có diện tích bằng nhau nên
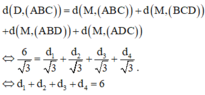

Kiểm tra các trường hợp chỉ có bốn điểm thỏa mãn.

Cho hình thang ABCD có diện tích 108cm2. Trên cạnh bên AD lấy 2 điểm M và N sao cho AM=MN=ND. Trên cạnh bên BC lấy 2 điểm E và G sao cho BE=EG=GC. Nối M với E và nối N với G được hình tứ giác MEGN. Tính diện tích hình tứ giác MEGN.
( Làm lời giải đầy đủ cho mình nhé, thks)
Cho hình thang ABCD có diện tích 2000cm2.trên canh bên AD lấy hai điểm Evà G sao chi AE=GD=AD/4.từ E và G kẻ các đường thẳng song song với hai đáy hình thang, cắt cạnh bên BC tại P và T khi ấy cũng có BP=TC=BC/4
a)tính diện tích hình tứ giác APCG
b)tính diện tích hình tứ giác EPTG
Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ 0 → mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD
A. 12
B. 4
C. 10
D. 8
Đáp án A.
Với mỗi cách chọn ra 2 đỉnh bất kỳ của tứ diện ta được 2 vecto đối nhau.
Do đó có 2 C 4 2 = 12 vecto.
Cho tứ diện ABCD, hỏi có bao nhiêu véctơ khác véctơ 0 → mà mỗi véctơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD
A. 4.
B. 12.
C. 10.
D. 8.
Đáp án là B
Mỗi cạnh của tứ diện tạo thành 2 vecto thỏa mãn đề bài, suy ra có 6.2 = 12 vecto.