Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có A trùng với gốc tọa độ O, các đỉnh B (m; 0; 0), D (0; m; 0), A’ (0; 0; n) với m, n 0 và m + n 4. Gọi M là trung điểm của cạnh CC’. Khi đó thể tích tứ diện BDA’M đạt giá trị lớn nhất bằng: A. 245/108 B. 9/4 C. 64/27 D. 75/32
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có A trùng với gốc tọa độ O, các đỉnh B (m; 0; 0), D (0; m; 0), A’ (0; 0; n) với m, n > 0 và m + n = 4. Gọi M là trung điểm của cạnh CC’. Khi đó thể tích tứ diện BDA’M đạt giá trị lớn nhất bằng:
A. 245/108
B. 9/4
C. 64/27
D. 75/32
Trong không gian với hệ tọa độ Oxy, cho hình hộp chữ nhật ABCD.ABCD có A trùng với gốc tọa độ O, các đỉnh B(m; 0; 0), D(0; m; 0), A(0; 0;n) với m, n0 và m+n4. Gọi M là trung điểm của cạnh CC. Khi đó thể tích tứ diện BDAM đạt giá trị lớn nhất bằng: A.
245
108
B.
9
4
C.
64...
Đọc tiếp
Trong không gian với hệ tọa độ Oxy, cho hình hộp chữ nhật ABCD.A'B'C'D' có A trùng với gốc tọa độ O, các đỉnh B(m; 0; 0), D(0; m; 0), A'(0; 0;n) với m, n>0 và m+n=4. Gọi M là trung điểm của cạnh CC'. Khi đó thể tích tứ diện BDA'M đạt giá trị lớn nhất bằng:
A. 245 108
B. 9 4
C. 64 27
D. 75 32
Trong không gian Oxyz, cho hai mặt cầu
(
S
1
)
:
x
2
+
y
2
+
z
2
-
2
x
+
4
y
-
2
z
+
2
0
và
(
S...
Đọc tiếp
Trong không gian Oxyz, cho hai mặt cầu ( S 1 ) : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z + 2 = 0 và ( S 2 ) : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z - 4 = 0 . Xét tứ diện ABCD có hai đỉnh A, B nằm trên S1; hai đỉnh C,D nằm trên S2. Thể tích khối tứ diện ABCD có giá trị lớn nhất bằng
A. 3 2
B. 2 3
C. 6 3
D. 6 2
Hình hộp chữ nhật ABCD.ABCD có AC
3
a; AB 2a; AD
5
a (a 0). Tính thể tích tứ diện ABDA. A. V
a
3
6
B. V
a
3
15
3
C. V
a
3
2
3...
Đọc tiếp
Hình hộp chữ nhật ABCD.A'B'C'D' có AC = 3 a; AB' = 2a; AD' = 5 a (a > 0). Tính thể tích tứ diện ABDA'.
A. V = a 3 6
B. V = a 3 15 3
C. V = a 3 2 3
D. V = a 3 3
Tìm các mặt phẳng đối xứng của các hình sau đây : a) Hình chóp tứ giác đều ; b) Hình chóp cụt tam giác đều ; c) Hình hộp chữ nhật mà không có mặt nào là hình vuông.
Trong Oxyz cho A(0; 2; 0); C(2; 0; 0); O’(0; 0; 3). Khi đó hình hộp OABC.O’A’B’C’ có bao nhiêu mặt phẳng đối xứng?
Đọc tiếp
Trong Oxyz cho A(0; 2; 0); C(2; 0; 0); O’(0; 0; 3). Khi đó hình hộp OABC.O’A’B’C’ có bao nhiêu mặt phẳng đối xứng?
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là A (-1; 0) và
C
(
m
;
m
)
, với m 0. Biết rằng đồ thị hàm số y
x
chia hình (H) thành hai phần có diện tích bằng nhau, tìm m .
Đọc tiếp
Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là A (-1; 0) và C ( m ; m ) , với m > 0. Biết rằng đồ thị hàm số y= x chia hình (H) thành hai phần có diện tích bằng nhau, tìm m .
![]()
![]()
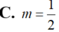
![]()
Cho tứ diện ABCD, hỏi có bao nhiêu véctơ khác véctơ 0 ⇀ mà mỗi véctơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD
A. 4.
B. 12.
C. 10.
D. 8.
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0; 4), D(4; 0; 6) Hãy viết phương trình của các mặt phẳng (ACD) và (BCD)




