Cho hình vẽ Chứng minh ba điểm B K C thẳng hàng

Những câu hỏi liên quan
Cho hình dưới (hình 65a). Chứng minh rằng ba điểm B, K, C thẳng hàng
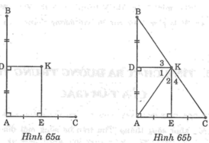
Nối KA, KB, KC (hình 65b).
Vì KD là đường trung trực của AB nên:
KA = KB (tính chất đường trung trực)
Suy ra: ΔKAB cân tại K
Do đó KD là đường phân giác của ∠(AKB)
Suy ra: ∠K1 = ∠K3 ⇒ ∠(AKB) = 2 ∠K1 (1)
Vì KE là đường trung trực của AC nên:
KA = KC (tính chất đường trung trực)
Do đó, tam giác AKC cân tại K. Suy ra KE là đường phân giác của ∠(AKC)
Suy ra: ∠K2 = ∠K4 ⇒ ∠(AKC) = 2 ∠K2 (2)
Ta có: KD ⊥ AB (gt) và AC ⊥ AB (gt)
Suy ra: KD // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song nhau)
Lại có: KE ⊥ AC (gt)
Suy ra: KE ⊥ KD (quan hệ giữa tính vuông góc và tính song song)
Hay: ∠(DKE) = 90o⇒ ∠K1 +∠K2 = 90o
Từ (1) và (2) suy ra: ∠(AKB) + ∠(AKC) = 2∠K1 + 2∠K2
= 2.( ∠K1 +∠K2 ) = 2.90o = 180o.
Vậy B, K, C thẳng hàng.
Đúng 0
Bình luận (0)
Cho góc nhọn xOy, trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Gọi H là trung điểm của đoạn thẳng AB.a) Chứng minh: ∆OAH ∆OBHb) Từ A vẽ đường thẳng vuông góc với OA, cắt tia OH tại C. Chứng minh: CB ⊥ OB.c) Gọi I là trung điểm đoạn thẳng OH, từ I vẽ đường thẳng vuông góc với OH, cắt tia OA tại M. Kẻ HK vuông góc với BC tại K. Chứng minh: ba điểm M, H, K thẳng hàng.có vẽ hình
Đọc tiếp
Cho góc nhọn xOy, trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi H là trung điểm của đoạn thẳng AB.
a) Chứng minh: ∆OAH = ∆OBH
b) Từ A vẽ đường thẳng vuông góc với OA, cắt tia OH tại C. Chứng minh: CB ⊥ OB.
c) Gọi I là trung điểm đoạn thẳng OH, từ I vẽ đường thẳng vuông góc với OH, cắt tia OA tại M. Kẻ HK vuông góc với BC tại K. Chứng minh: ba điểm M, H, K thẳng hàng.
có vẽ hình
a) Xét ΔOAHΔOAH và ΔOBHΔOBH ta có:
OA = OB (theo giả thiết)
HA = HB (H là trung điểm AB)
OH chung
⇒ΔOAH=ΔOBH(c−c−c)⇒ΔOAH=ΔOBH(c−c−c)
b) Ta có: ΔOAH=ΔOBHΔOAH=ΔOBH (chứng minh trên)
⇒∠AOH=∠BOH⇒∠AOH=∠BOH ( 2 góc tương ứng bằng nhau)
Hay ∠AOC=∠BOC∠AOC=∠BOC
Xét ΔOACΔOAC và ΔOBCΔOBC ta có:
OA = OB (theo giả thiết)
OC chung
∠AOC=∠BOC∠AOC=∠BOC
⇒ΔOAC=ΔOBC(c−g−c)⇒ΔOAC=ΔOBC(c−g−c)
⇒∠OAC=∠OBC⇒∠OAC=∠OBC(2 góc tương ứng)
Mà ∠OAC∠OAC= 900 nên ∠OBC∠OBC = 900
⇒CB⊥OB⇒CB⊥OB( điều phải chứng minh)
c) Ta có: ∠AOC=∠BOC∠AOC=∠BOC (chứng minh trên) (1)
Xét 2 tam giác vuông MIO và MIH ta có:
MI chung
IO = IH (Vì I là trung điểm của OH)
⇒ΔMIO=ΔMIH⇒ΔMIO=ΔMIH (Cạnh góc vuông – cạnh góc vuông)
⇒∠MOI=∠MHI⇒∠MOI=∠MHI (2 góc tương ứng)
Hay∠AOC=∠MHIHay∠AOC=∠MHI (2)
Từ (1) và (2) ta có: ∠BOC=∠MHI∠BOC=∠MHI (cặp góc ở vị trí so le trong)
⇒MH//OB⇒MH//OB (*)
Lại có:
HK⊥BCOB⊥BC}⇒HK//OBHK⊥BCOB⊥BC}⇒HK//OB (Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng) (**)
Từ (*) và (**) ta có: MH và HK cùng thuộc một đường thẳng song song với OB.
Suy ra M, H, K thẳng hàng (điều phải chứng minh)
a) Xét tam giác AHO và tam giác BHO
có OH chung
HA=HB (GT)
OA=OB (GT)
suy ra tam giác AHO = tam giác BHO (c.c.c) (1)
b) Từ (1) suy ra góc AOC = góc BOC
Xét tam giác AOC và tam giác BOC có
OC chung
góc AOC = góc BOC
OA=OB (GT)
suy ra tam giác AOC = tam giác BOC (c.g.c)
suy ra góc OAC = góc OBC (hai góc tương ứng)
mà góc OAC =900
suy ra góc OBC = 900
suy ra CB vuông góc với OB tại B
a , Cho ba điểm H , I , K thẳng hàng thì có mấy trường hợp vẽ ? Hãy vẽ hình minh họa từng trường hợp
b , Trong mỗi trường hợp , có mấy điểm nằm giữa hai điểm còn lại
c , Hãy nói cách vẽ ba điểm không thẳng hàng
Cho hình thang ABCD (AB//CD) gọi E , F , K lần lượt là trung điểm của Ad , AC , BC a) Chứng minh EF//CD b) Chứng minh EK//CD c) Chứng minh ba điểm E,F,K thẳng hàng
Cho 5 điểm A, B, C, M và N thỏa mãn: ba điểm A, B, C thẳng hàng, ba điểm A, B, Mkhông thẳng hàng và ba điểm A, B, N thẳng hàng.
A, vẽ hình minh họa
B, chứng tỏ bốn điểm A, B, Cvà N cùng thuộc một đường thẳng
C, có bao nhiêu đường thẳng phân biệt đi qua hai điểm trong 5 điểm đã cho? Kể tên
Tính tổng các số nguyên x biết :
1, -20<x<21
2, -18< -x<- 17
3,-27<x<-27
4, |x|<-3
5, |-x|<5
Mọi người giúp mình với HELP ME
vẽ năm điểm : A , B , C , D , E sao cho ba điểm A , B , C thẳng hàng ba điêm B , C , D thẳng hàng , ba điểm C,D,E không thẳng hàng . Chứng minh bốn điểm A,B,C,D thẳng hàng
Cho tam giác ABC vuông tại A ( AB<AC) và M, N , I lần lượt là trung diểm của AB , AC , BC
a, Chứng minh tứ giác BMNI là hình bình hành
b, vẽ điểm E đối xứng với I qua N Chứng minh tứ giác AICE là hình thoi
c, Vẽ điểm K đối xứng với I qua M . Chứng minh ba điểm K, A, E thẳng hàng
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:a) Tứ giác AHFK là hình chữ nhật;b) AF song song với BD;c) Ba điểm E, H, K thẳng hàng
Đọc tiếp
Cho hình chữ nhật ABCD. Nối C với một điểm E bất kỳ trên đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho EF = EC. Vẽ FH và FK lần lượt vuông góc với đường thẳng AB và AD tại h và K. Chứng minh rằng:
a) Tứ giác AHFK là hình chữ nhật;
b) AF song song với BD;
c) Ba điểm E, H, K thẳng hàng
a) F H A ^ = H A K ^ = A K F ^ = 90 0
Þ AHFK là hình chữ nhật.
b) Gọi là giao điểm của AC và BD. Chứng minh OE là đường trung bình của DACF
Þ AF//OE
Þ AF/BD
c) Gọi I là giao điểm của AF và HK.
Chứng minh
H 1 ^ = A ^ 1 ( H 1 ^ = A 2 ^ = B 1 ^ = A 1 ^ ) ⇒ K H / / A C mà KH đi qua trung điểm I của AF Þ KH đi qua trung điểm của FC.
Mà E là trung điểm của FC Þ K, H, E thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại B. Có E,D lần lượt là trung điểm của các cạnh AC và BC.
a) Gọi F là điểm đối xứng của E qua D. Chứng minh : Tứ giác BECF là hình thoi.
b) Vẽ H là hình chiếu của E trên AB. Chứng minh: Tứ giác HEDB là hình chữ nhật.
c) Lấy G là giao điểm của BE và CH, K là trung điểm của EH. Chứng minh: Ba điểm A,K,G thẳng hàng.















