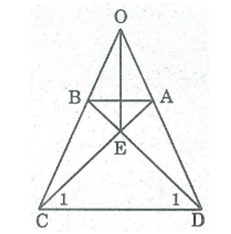
Bài 1: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OAOB , OCOD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Bài 2: Cho hình thang ABCD (AD//BC, ADBC) có đường chéo AC vuông góc với cạnh bên CD, AC là tia phân giác góc BAD và góc D60 độ
a) Chứng minh ABCD là hình thang cân
b) Tính độ dài cạnh AD, biết chu vi hình th...
Đọc tiếp
Bài 1: Cho hình thang cân ABCD có AB//CD, O là giao điểm của hai đường chéo, E là giao điểm của hai đường thẳng chứa cạnh bên AD và BC. Chứng minh:
a) OA=OB , OC=OD
b) EO là đường trung trực của hai đáy hình thang ABCD.
Bài 2: Cho hình thang ABCD (AD//BC, AD>BC) có đường chéo AC vuông góc với cạnh bên CD, AC là tia phân giác góc BAD và góc D=60 độ
a) Chứng minh ABCD là hình thang cân
b) Tính độ dài cạnh AD, biết chu vi hình thang bằng 20cm.
Bài 3: Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD=AE
a) Tứ giác BDEC là hình gì ? Vì sao?
b) Các điểm D,E ở vị trí nào thì BD=DE=EC?
Mình đang cần gấp. Giúp mình nhé cảm ơn các bạn