Question

Hình thang cân ABCD có 0 là giao điểm của hai đường thắng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.

Answer 1

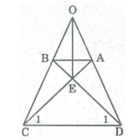
Ta có:  ∠ (ADC) = ∠ (BCD) (gt)

⇒  ∠ (ODC) =  ∠ (OCD)

⇒ ∆ OCD cân tại O

⇒ OC = OD

OB + BC = OA + AD

Mà AD = BC (tính chất hình thang cân)

⇒ OA = OB

Xét  ∆ ADC và ∆ BCD:

AD = BC (tính chất hình thang cân )

AC = BD (tính chất hình thang cân)

CD chung

Do đó  ∆ ADC và ∆ BCD (c.c.c)

⇒  ∠ D 1 = ∠ C 1

⇒ ∆ EDC cân tại E

⇒ EC = ED nên E thuộc đường trung trực CD

OC = OD nên O thuộc đường trung trực CD

E ≠ O. Vậy OE là đường trung trực của CD.

Ta có: BD= AC (tính chất hình thang cân)

⇒ EB + ED = EA + EC mà ED = EC

⇒ EB = EA nên E thuộc đường trung trực AB

OA = OB (chứng minh trên ) nên O thuộc đường trung trực của AB

E  ≠  O. Vậy OE là đường trung trực của AB.