tìm xy thỏa
xyxy=xy2 + yx2
Những câu hỏi liên quan
x
2
+
x
y
x
3
+
x
2
y
+
x
y
2
+
y
3...
Đọc tiếp
x 2 + x y x 3 + x 2 y + x y 2 + y 3 + y x 2 + y 2 : 1 x - y - 2 x y x 3 - x 2 y + x y 2 - y 3
II. PHẦN TỰ LUẬN:Dạng 1: Thu gọn đơn thức rồi tìm hệ sô, phần biến của đơn thức thu được: d) xy2 . ( x3y) . ( - 3x13y5 )0e) g) (-6x3zy)( yx2)2 h) i) k) () .()
Đọc tiếp
II. PHẦN TỰ LUẬN:
Dạng 1: Thu gọn đơn thức rồi tìm hệ sô, phần biến của đơn thức thu được:
d) 
xy2 . ( x3y) . ( - 3x13y5 )0
e) 
g) (-6x3zy)( 
yx2)2 h) 
i) 
k) (
) .(
)
Hệ phương trình
x
−
1
y
2
+
6
y
x
2...
Đọc tiếp
Hệ phương trình x − 1 y 2 + 6 = y x 2 + 1 y − 1 x 2 + 6 = x y 2 + 1 có bao nhiêu cặp nghiệm (x; y) mà x > y
A. 1
B. 4
C. 2
D. 3
Hệ đã cho ⇔ x y 2 + 6 x − y 2 − 6 = y x 2 + y y x 2 + 6 y − x 2 − 6 = x y 2 + x
Trừ vế theo vế hai phương trình của hệ ta được:
2xy(y – x) +7 (x – y) + (x – y) (x + y) = 0
⇔ (x – y)(x + y – 2xy + 7) = 0 x = y x + y − 2 x y + 7 = 0
+ Nếu x = y thay vào hệ ta có: x 2 – 5 x + 6 = 0 ⇔ x = y = 2 x = y = 3
+ Nếu x + y – 2xy + 7 = 0 ⇔ 2x + 2y – 4xy + 14 = 0
⇔ (2x – 1) + 2y (1 – 2x) = −15 ⇔ (1 – 2x) (1 – 2y) = 15
Mặt khác khi cộng hai phương trình của hệ đã cho ta được:
x 2 + y 2 – 5 x – 5 y + 12 = 0 ⇔ 4 x 2 – 20 x + 25 + 4 y 2 – 20 y + 25 – 2 = 0
⇔ ( 2 x – 5 ) 2 + ( 2 y – 5 ) 2 = 2 ⇔ ( 2 x – 5 ) 2 + ( 2 y – 5 ) 2 = 2
Đặt a = 2x – 5; b = 2y – 5
Ta có a 2 + b 2 = 2 a + 4 b + 4 = 14
⇔ a + b 2 − 2 a b = 2 a b + 4 a + b = − 1 ⇔ a + b = 0 a b = − 1 a + b = − 8 a b = 31
Trường hợp 1: a + b = 0 a b = − 1 ⇔ (x; y) = (3; 2), (2; 3)
Trường hợp 2: a + b = − 8 a b = 31 vô nghiệm
Vậy nghiệm của hệ đã cho là (x; y) {(2; 2); (3; 3); (2; 3); (3; 2)}
Suy ra có một cặp nghiệm thỏa mãn yêu cầu bài toán là (x; y) = (3; 2)
Đáp án:A
Đúng 0
Bình luận (0)
Tìm mẫu thức chung của hai phân thức sau:
x
-
y
x
2
+
x
y
;
2
x
-
3
y
x
y
2
A.
x
y
2
(
x
+
y...
Đọc tiếp
Tìm mẫu thức chung của hai phân thức sau: x - y x 2 + x y ; 2 x - 3 y x y 2
A. x y 2 ( x + y )
B. x y 2
C. x y 2 ( x + 1 )
D. xy(x + y + 1)
Tìm xy-xy2=3
Xét các số thực dương x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-
3...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất Pmax của P = 3 x + 2 y + 1 x + y + 6 .
A. 3.
B. 2.
C. 1.
D. 4.
Đáp án C.
Ta có
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 - 3 x + y - 2
⇔ log 3 x + y - log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 - 3 x + y - 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ , có f ' t = 1 + 1 t ln 3 > 0 ; ∀ t > 0 .
Suy ra f(t) là hàm số đồng biến trên 0 ; + ∞ mà f[3(x + y)] = f(x2 + y2 + xy + 2)
Đúng 0
Bình luận (0)
Xét các số thực dương x,y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
−
3...
Đọc tiếp
Xét các số thực dương x,y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x − 3 + y y − 3 + x y . Tìm giá trị lớn nhất P m a x của P = 3 x + 2 y + 1 x + y + 6 .
A. 3
B. 2
C. 1
D. 4
Đáp án C.
Ta có x x − 3 + y y − 3 + x y
= x 2 + y 2 + x y − 3 x − 3 y = x 2 + y 2 + x y + 2 − 3 x + y − 2
Khi đó, giả thiết trở thành:
log 3 x + y x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ log 3 x + y − log 3 x 2 + y 2 + x y + 2 = x 2 + y 2 + x y + 2 − 3 x + y − 2
⇔ 3 x + y + log 3 3 x + y = x 2 + y 2 + x y + 2 + log 3 x 2 + y 2 + x y + 2
Xét hàm số f t = t + log 3 t trên khoảng 0 ; + ∞ ,
có f ' t = 1 + 1 t ln 3 > ; ∀ t > 0.
Suy ra f( t) là hàm số đồng biến trên 0 ; + ∞
mà f 3 x + y = f x 2 + y 2 + x y + 2
⇔ 2 x + y 2 − 6 2 x + y + 5 = − 3 y − 1 2 ≤ 0 ⇔ 1 ≤ 2 x + y ≤ 5.
Khi đó P = 1 + 2 x + y − 5 x + y + 6 ≤ 1
vì 2 x + y − 5 ≤ 0 x + y + 6 > 0 . Vậy P m a x = 1.
Đúng 0
Bình luận (0)
Cho hai số thực x, y thỏa mãn
log
3
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-
3...
Đọc tiếp
Cho hai số thực x, y thỏa mãn log 3 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất của biểu thức P = x + 2 y + 3 x + y + 6
Xét các số thực dương x, y thỏa mãn
log
5
x
+
y
x
2
+
y
2
+
x
y
+
2
x
x
-
3...
Đọc tiếp
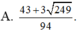
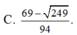
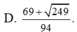
Xét các số thực dương x, y thỏa mãn log 5 x + y x 2 + y 2 + x y + 2 = x x - 3 + y y - 3 + x y . Tìm giá trị lớn nhất của biểu thức P = 3 x + 2 y + 1 x + y + 6 .
A. m a x P = 1
B. m a x P = 4
C. m a x P = 2
D. m a x P = 3
Chọn A.
Phương pháp:
- Biến đổi điều kiện bài cho về dạng f u = f v với u, v là các biểu thức của x, y.
- Xét hàm f t suy ra mối quan hệ của u, v rồi suy ra x, y.
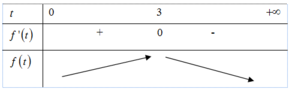
- Đánh giá P theo biến t=x+y bằng cách sử dụng phương pháp hàm số.
Cách giải:
Đúng 0
Bình luận (0)
Cho x,y là hai số thực dương thay đổi thỏa mãn điều kiện
(
x
y
+
1
)
(
x
y
+
1
-
y
)
≤
1
-
x
-
1
y
. Tìm giá trị lớn nhấ...
Đọc tiếp
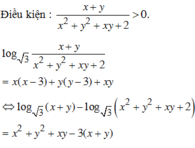
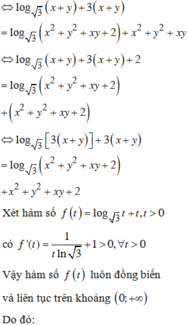
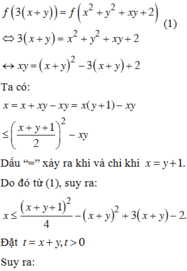
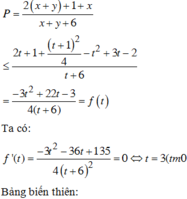
Cho x,y là hai số thực dương thay đổi thỏa mãn điều kiện ( x y + 1 ) ( x y + 1 - y ) ≤ 1 - x - 1 y . Tìm giá trị lớn nhất của biểu thức P = x + y x 2 - x y + 3 y 2 - x - 2 y 6 ( x + y )
A. 5 3 - 7 30
B. 7 30 - 5 3
C. 5 3 + 7 30
D. 5 + 7 30
