Cho hình thang ABCD. Gọi M là trung điểm của CD. AM cắt BD tại E. BE=6cm, ED=8cm, DM=10cm. Tính AB

Những câu hỏi liên quan
Cho hình thang ABCD (AB CD. AM cắt BD tại E. al Nếu BE=6cm; ED=8cm; DM=10cm. Tính độ dài AB? b/ AC cắt BM ở F. Chứng minh EF//AB. c/ Đường thắng EF cắt AD, BC ở H và K. Chứng minh HF = 2FK.
a:
Sửa đề; EA=6cm
Xét ΔEMD và ΔEBA có
góc EMD=góc EBA
góc MED=góc BEA
=>ΔEMD đồng dạng vơi ΔEBA
=>MD/BA=ED/EA
=>10/BA=8/6=4/3
=>BA=7,5cm
b: Xét ΔFMC và ΔFBA có
góc FMC=góc FBA
góc MFC=góc BFA
=>ΔFMC đồng dạng với ΔFBA
=>FM/FB=MC/BA=MD/BA=EM/EA
=>FE//AB
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB CD. AM cắt BD tại E.
al Nếu BE=6cm; ED=8cm; DM=10cm. Tính độ dài AB?
b/ AC cắt BM ở F. Chứng minh EF//AB.
c/ Đường thắng EF cắt AD, BC ở H và K. Chứng minh HF = 2FK.
Cho hình thang ABCD(AB//CD), AC cắt BD tại O
a, chứng minh:OA.OD=OB.OC. Nếu AB=4cm, DC=8cm, DC=6cm. Tính OA?
b, Gọi M là trung điểm BC,AM cắt BD tại I, BM cắt AC tại K. Chứng minh:IK//AB
cho hình thang ABCD(AB//CD)có AB=3cm, CD=7cm, AD=10cm. Gọi M là trung điểm của BC. Gọi E là giao điểm của AM và CD. CMR: AM vuông góc với DM
Cho hình chữ nhật ABCD , BH⊥AC , BM⊥AC.a, C/m ΔABH đồng dạng với ΔACB và AC. AH AB2b, Cho AB8cm , BC6cm. Tính AC,AB,CHc, I đối xứng với B qua AC. C/m DMIH và ACID là hình thang când, E,F là trung điểm của AH,CD . BF cắt AC tại K. C/m BF.EK ≥ BE.BF(Caccau giúp mình với ạ)
Đọc tiếp
Cho hình chữ nhật ABCD , BH⊥AC , BM⊥AC.
a, C/m ΔABH đồng dạng với ΔACB và AC. AH = AB2
b, Cho AB=8cm , BC=6cm. Tính AC,AB,CH
c, I đối xứng với B qua AC. C/m DM=IH và ACID là hình thang cân
d, E,F là trung điểm của AH,CD . BF cắt AC tại K. C/m BF.EK ≥ BE.BF
(Caccau giúp mình với ạ)
![]()
b) Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=AB^2+BC^2\)
\(\Leftrightarrow AC^2=8^2+6^2=100\)
hay AC=10(cm)
Vậy: AC=10cm
Đúng 2
Bình luận (0)
Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.
a) Chứng minh rằng AK = KC, BI = ID.
b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.
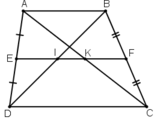
a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD.
⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt)
⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt)
⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB
⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF
⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm
Đúng 2
Bình luận (0)
Cho hình thang ABCD (AB//CD). M là trung điểm của CD. AM cắt BD tại I. BM cắt AC tại K. KI cắt BD, BC lần lượt tại E là F. Gọi N là trung điểm của AB, O là giao điểm của AC và BD. Chứng minh M, O, N thẳng hàng.
. Cho hình thang cân ABCD (AB//CD và AB<CD) Kẻ các đường cao AH và BK của hình thang.CM: a; DH=CK
b; Gọi M là trung điểm của AD và N là trung điểm của BC.MN lần lượt cắt BD tại E và AC tại F.Biết AB=4cm,CD=10cm,tính EF ?
xét tg ADH và tg BCK có: ^AHD=^BKC=90 ; AD=BC( vì tg ABCD là hthang cân); ^ADH =^BCK (vì tg ABCD là hthang cân)
=> tg ADH=tg BCK (ch-gn) => DH=CK
b) xét hthang ABCD có: M là t/đ của AD(gt) và N là t/đ của BC(gt)=> MN là đg trung bình của hthang ABCD => MN//AB//CD
và MN= 1/2.(AB+CD)=> MN= 1/2.(4+10)==7 (cm)
xét tg ABC có: N là t/đ của Bc(gt) ; NF//AB( vì F thuộc MN ; MN//AB) => F là t/đ của AC=> NF la đg trung bình của tg ABC
=> NF=1/2.AB=1/2.4=2(cm)
c/m tương tự ta đc: ME=2cm
ta có: MN=ME+EF+FN ( vì E,F thuộc MN)
=> 7 =2+EF+2 => EF=3 (cm)
Vậy độ dài cạnh EF là 3cm
Đúng 0
Bình luận (0)
Cho hình thang ABCD vuông tại A và B có D = 45o, BC = 6cm, AB = 8cm. a) Tính AD, CD. b) Gọi M, N, E, F là trung điểm của AB, CD, BD, AC. Chứng minh M, N, E, F thẳng hàng. Mong anh chị giúp em câu a, b ạ.
















