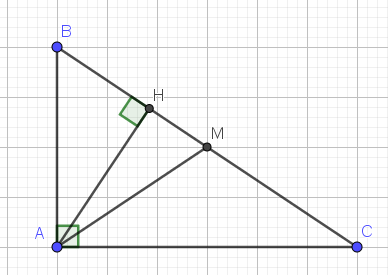
cho tam giác ABC vuông tại A có AB bằng 12cm . BC bằng 20cm . Vẽ đường cao AH . Đường phân giác AD hỏi : Tính AH VÀ BH . nhanh nha mn mk đang cần gấp ó

Những câu hỏi liên quan
Bài 1 Cho tam giác ABC vuông tại A có đường cao AH cho AB5cm,BH3cma)Tính BC,AHb) Kẻ HE vuông góc vs AC .Tính HEBài 2Cho tam giác ABC vuông tại A đường cao AH phân giác AD biết BD10cm,DC20cm.Tính AH,HDBaif3a) cho tam giác ABC vuông tại A có AB5cm đg cao AH4cm. Tính chu vi tam giác ABCb) cho tam giác ABC vuông tại A đg cao AH phân giác AD.biết BD 15cm DC20cm Tính AH,ADGiải nhanh giúp mk nha mk c.ơn
Đọc tiếp
Bài 1
Cho tam giác ABC vuông tại A có đường cao AH cho AB=5cm,BH=3cm
a)Tính BC,AH
b) Kẻ HE vuông góc vs AC .Tính HE
Bài 2
Cho tam giác ABC vuông tại A đường cao AH phân giác AD biết BD=10cm,DC=20cm.Tính AH,HD
Baif3
a) cho tam giác ABC vuông tại A có AB=5cm đg cao AH=4cm. Tính chu vi tam giác ABC
b) cho tam giác ABC vuông tại A đg cao AH phân giác AD.biết BD =15cm DC=20cm Tính AH,AD
Giải nhanh giúp mk nha mk c.ơn
BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= ![]() =
= ![]()
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= ![]() =4 (cm)
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:

· ![]()
Đúng 0
Bình luận (0)
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)
Đúng 0
Bình luận (0)
Tui đag cần gấp mg mn giúp đỡ ạ ! Câu1 Cho tam giác ABC vuông tại A, đường cao AH a)Cho AH bằng 16,BH bằng 25 . Tính AB,AC,BC,CH b)Cho AB bằng 12,BH bằng 6.Tính AH,AC,BC,CH Câu 2 Cho tam giác ABC vuông tại A.Biết rằng AB/AC=5/6 đường cao AH=30cm. Tính HB và HC
Câu 2:
AB/AC=5/6
=>HB/HC=25/36
=>HB/25=HC/36=k
=>HB=25k; HC=36k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>900k^2=900
=>k=1
=>HB=25cm; HC=36cm
Đúng 0
Bình luận (0)
1, Cho tam giác ABC ( góc A90 độ). Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với cạnh huyền BC tại D. C/m: BD^2-CD^2AB^22, Cho tam giác ABC( góc A90 độ). phân giác AD, đường cao AH. biết BD15cm, CD20cm, tính BH, CH3, Cho tam giác ABC( góc A90 độ). AB12cm, AC16cm, phân giác AD, đường cao AH. tính HB,HC,HD4, Cho tam giác ABC( góc A90 độ) đường cao AH. Tính chu vi tam giác ABC biết AH 14 cm, HB/HC1/4giúp đỡ mình nhé, mình đang cần gấp
Đọc tiếp
1, Cho tam giác ABC ( góc A=90 độ). Từ trung điểm I của cạnh AC kẻ đường thẳng vuông góc với cạnh huyền BC tại D. C/m: BD^2-CD^2=AB^2
2, Cho tam giác ABC( góc A=90 độ). phân giác AD, đường cao AH. biết BD=15cm, CD=20cm, tính BH, CH
3, Cho tam giác ABC( góc A=90 độ). AB=12cm, AC=16cm, phân giác AD, đường cao AH. tính HB,HC,HD
4, Cho tam giác ABC( góc A=90 độ) đường cao AH. Tính chu vi tam giác ABC biết AH= 14 cm, HB/HC=1/4
giúp đỡ mình nhé, mình đang cần gấp
3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 12cm, AC =16cm. Vẽ đường cao AH.
a) Cm tam giác HBA đồng dạng tam giác ABC.
b) Tính BC,AH,BH.
c)Vẽ đường phân giác AD của tam giác ABC( D thuộc BC).Tính BD,CD
Tự vẽ hình nha
a) xét tam giác HAB và tam giác ABC
góc AHB = góc ABC
góc CAB : chung
Suy ra : tam giác AHB ~ tam giác ABC ( g-g )
b) Áp dụng định lí py - ta - go vào tam giác ABC ta được :
AC2 + AB2 = BC2
162 + 122 = BC2
400 = BC2
=> BC = \(\sqrt{400}\)= 20 ( cm )
ta có tam giác HAB ~ tam giác ABC ( câu a )
=> \(\frac{AH}{AC}=\frac{AB}{BC}hay\frac{AH}{16}=\frac{12}{20}\)
=> AH = \(\frac{12.16}{20}=9,6\)( cm )
Độ dài cạnh BH là
Áp dụng định lí py - ta - go vào tam giác HBA ta được :
AH2 + BH2 = AB2
BH2 = AB2 - AH2
BH2 = 122 - 9,62
BH2 = 51,84
=> BH = \(\sqrt{51,84}\) = 7,2 ( cm )
c) Vì AD là đường phân giác của tam giác ABC nên :
\(\frac{AB}{BD}=\frac{AC}{CD}\Leftrightarrow\frac{AB}{BC-CD}=\frac{AC}{CD}\)
<=> \(\frac{AB.CD}{CD\left(BC-CD\right)}=\frac{AC\left(BC-CD\right)}{CD\left(BC-CD\right)}\)
<=> AB.CD = AC(BC - CD)
hay 12CD = 16.20 - 16CD
<=> 12CD+ 16CD = 320
<=> 28CD = 320
<=> CD = \(\frac{320}{28}\approx11.43\left(cm\right)\)
Độ dài cạnh BD là :
BD = BC - CD
BD = 20 - \(\frac{320}{28}\)\(\approx\) 8,57 ( cm )
Đúng 0
Bình luận (0)
Cho hỏi đồng dạng là sao bạn???Tớ mới học lớp 7 thôi,nên chưa biết ^^
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
Bài 1: Cho tam giác ABC vuông tại A, phân giác AD, đường cao AH. Biết BD = 15cm; DC = 20cm. Tính AB, AC, AH,AD.
Bài 2: Cho tam giác ABC vuông tại A, phân giác AD, đường cao AH. Biết AB=12cm; AC = 16cm. Tính HD,HB.HC.
Bài 3: Cho tam giác ABC vuông tại A, phân giác AD, đường cao AH. Biết AB=24cm; AC = 32cm. Tính HD,HB,HC.
1:
BC=15+20=35cm
AD là phân gíac
=>AB/BD=AC/CD
=>AB/3=AC/4=k
=>AB=3k; AC=4k
AB^2+AC^2=BC^2
=>25k^2=35^2
=>k=7
=>AB=21cm; AC=28cm
AH=21*28/35=16,8cm
\(AD=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)
2:
BC=căn 12^2+16^2=20cm
HB=AB^2/BC=12^2/20=7,2cm
HC=20-7,2=12,8cm
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AH là đường cao, AB= 12cm, BC= 20cm. Tính BH, HC?
Xét tam giác ABC vuông tại A ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-12^2}=16\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}BH\cdot BC=AB^2\\HC\cdot BC=AC^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7,2\left(cm\right)\\HC=\dfrac{AC^2}{BC}=\dfrac{16^2}{20}=12,8\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a (ab < ac) đường cao ah.biết ah bằng 12cm,bc bằng 25cm
a, tính bh,hc,ab và ac
b, vẽ trung tuyến am.tính góc amh
c,tính diện tích tam giác amh
Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông:
$144=AH^2=BH.HC(1)$
$BH+CH=BC=25(2)$
Từ $(1); (2)$ áp dụng định lý Viet đảo thì $BH, CH$ là nghiệm của pt: $x^2-25x+144=0$
$\Rightarrow BH, CH= (16,9)$
Mà $AB< AC$ nên $BH< CH$
$\Rightarrow BH=9; CH=16$ (cm)
$AB=\sqrt{BH^2+AH^2}=\sqrt{9^2+12^2}=15$ (cm)
$AC=\sqrt{CH^2+AH^2}=\sqrt{16^2+12^2}=20$ (cm)
b.
$AM=\frac{BC}{2}=\frac{25}{2}$ (cm)
$\sin \widehat{AMH}=\frac{AH}{AM}=\frac{24}{25}$
$\Rightarrow \widehat{AMH}\approx 74^0$
c.
$HM=\sqrt{AM^2-AH^2}=\sqrt{(\frac{25}{2})^2-12^2}=3,5$ (cm)
$S_{AHM}=\frac{AH.HM}{2}=\frac{12.3,5}{2}=21$ (cm2)
Đúng 1
Bình luận (0)
cho ABC vuông tại A có BC dài 20cm, góc C bằng 40°. Đường cao AH hãy Tính AB,AC,AH,BH và diện tích tam giác ABC
Cho tam giác ABC vuông tại A có AB = 12cm, AC =16cm. Vẽ đường cao AH.
a) Cm tam giác HBA đồng dạng tam giác ABC.
b) Tính BC,AH,BH.
c)Vẽ đường phân giác AD của tam giác ABC( D thuộc BC).Tính BD,CD
d) Trên AH lấy điểm K sao cho AK=3,6cm. Từ K kẻ đường thẳng song song BC cắt AB ,AC lần lượt tại M, N.
Tính diện tích tứ giác BMNC.