Tìm tất cả các giá trị của x,y thỏa mãn:
y2+2y+4x-2x+1+2=0
Những câu hỏi liên quan
1:tìm tất cả các giá trị của x thỏa mãn |x+1|-2|x-1|-x=0
2:tìm tất cả các giá trị của x, y thỏa mãn | x-2|-|4x-8|-y^2=0
giúp mình nhé!mình cần gấp
tìm tất cả các giá trị nguyên dương của x;y thỏa mãn
\(\frac{4x^2-4x+7}{x^2+1}=2+2y-y^2\)
\(VP=3-\left(y^2-2y+1\right)=3-\left(y-1\right)^2\le3\)(Dấu "=" xảy ra khi \(y=1\)
Nhìn đề bài ta đoán dạng bất đẳng thức, có \(VP\le3\), giờ ta chứng minh \(VT\ge3\)
Thật vậy, ta có
\(\frac{4x^2-4x+7}{x^2+1}-3=\frac{4x^2-4x+7-3\left(x^2+1\right)}{x^2+1}=\frac{x^2-4x+4}{x^2+1}\)
\(=\frac{\left(x-2\right)^2}{x^2+1}\ge0\)
Do đó; \(\frac{4x^2-4x+7}{x^2+1}\ge3\)(dấu "=" xảy ra khi \(x=2\))
\(\Rightarrow\frac{4x^2-4x+7}{x^2+1}\ge3\ge2+2y-y^2\)
\(VT=VP\Leftrightarrow VT=3;VP=3\)
\(\Leftrightarrow x=3;y=1\)
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
(
2
x
+
2
y
+
5
)
≥
1
giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m 0 thuộc tập nào sau đây?
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 ( 2 x + 2 y + 5 ) ≥ 1 giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m = 0 thuộc tập nào sau đây?
Đáp án A
Ta có, giả thiết
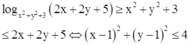
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của x, y thỏa mãn đẳng thức: y2 + 2y + yx - 2x + 1 + 2 = 0.
Câu 1: Giải phương trình và hệ phương trìnha) sqrt{4x^2-4x+9}3b) left{{}begin{matrix}3x-y52y-x0end{matrix}right.Câu 2:a) Cho hai đường thẳng (d_1): y 2x - 5 và (d_2): y 4x - m (m là tham số). Tìm tất cả các giá trị của tham số m để (d_1) và (d_2) cắt nhau tại một điểm trên trục hoành Oxb) Rút gọn biểu thức: Pleft(dfrac{sqrt{x}}{3+sqrt{x}}+dfrac{2x}{9-x}right):left(dfrac{sqrt{x}-1}{x-3sqrt{x}}-dfrac{2}{sqrt{x}}right) với x 0, x ne 9, x ne 25
Đọc tiếp
Câu 1: Giải phương trình và hệ phương trình
a) \(\sqrt{4x^2-4x+9}=3\)
b) \(\left\{{}\begin{matrix}3x-y=5\\2y-x=0\end{matrix}\right.\)
Câu 2:
a) Cho hai đường thẳng (d\(_1\)): y = 2x - 5 và (d\(_2\)): y = 4x - m (m là tham số). Tìm tất cả các giá trị của tham số m để (d\(_1\)) và (d\(_2\)) cắt nhau tại một điểm trên trục hoành Ox
b) Rút gọn biểu thức: \(P=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\) với x > 0, x \(\ne\) 9, x \(\ne\) 25
a) \(\sqrt{4x^2-4x+9}=3\)
Vì \(4x^2-4x+9=\left(2x-1\right)^2+8>0\)( Với mọi x )
Nên \(\sqrt{4x^2-4x+9}=3\)
⇔\(4x^2-4x+9=9\)
⇔\(4x^2-4x=0\)
⇔\(4x\left(x-1\right)=0\)
⇔\(\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)là nghiệm
Đúng 2
Bình luận (0)
Học sinh lớp 7 năm nay lên lớp 8 mới làm quen hằng đẳng thức mong các bạn giúp mình !!!
Tìm tất cả các giá trị của x,y thỏa mãn đẳng thức :
a)y2+2y+4x-2x+1+2=0
b)5x2+5y2+8xy-2x+2y+2=0
\(a\text{) }pt\Leftrightarrow\left(y^2+2y+1\right)+\left[\left(2^x\right)^2-2.2^x+1\right]=0\)
\(\Leftrightarrow\left(y+1\right)^2+\left(2^x-1\right)^2=0\)
\(\Leftrightarrow y+1=0\text{ và }2^x-1=0\)
\(\Leftrightarrow y=-1\text{ và }x=0\)
\(b\text{) }pt\Leftrightarrow\left(4x^2+4y^2+8xy\right)+\left(x^2-2x+1\right)+\left(y^2+2y+1\right)=0\)
\(\Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
\(\Leftrightarrow x+y=0\text{ và }x-1=0\text{ và }y+1=0\)
\(\Leftrightarrow x=1\text{ và }y=-1\)
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x; y) thỏa mãn
log
x
2
+
y
2
+
2
(
4
x
+
4
y
-
4
)
≥
1
. Tìm m nhỏ nhất để tồn tại duy nhất cặp (x; y) sao cho
x
2
+
y...
Đọc tiếp
Trong tất cả các cặp (x; y) thỏa mãn log x 2 + y 2 + 2 ( 4 x + 4 y - 4 ) ≥ 1 . Tìm m nhỏ nhất để tồn tại duy nhất cặp (x; y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0
A. ( 10 - 2 ) 2
B. 10 + 2
C. ( 10 + 2 ) 2
D. 10 - 2
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
2
x
+
2
y
+
5
≥
1
, giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho...
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ 1 , giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x 2 + y 2 + 4 x + 6 y + 13 - m = 0 thuộc tập nào sau đây?
A. [8;10]
B. [5;7]
C. [1;4]
D. [-3;0]
Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
4
x
–
m
.
2
x
+
1
0
có hai nghiệm
x
1
,
x
2
thỏa
x
1
+
x
2
1
A. m ≥ 2 B. mÎR C. m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 4 x – m . 2 x + 1 = 0 có hai nghiệm x 1 , x 2 thỏa x 1 + x 2 = 1
A. m ≥ 2
B. mÎR
C. m = 0
D. m ≥ 2 ; m ≤ -2
