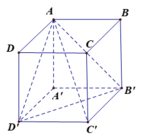
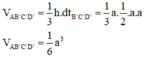Cho hình lập phương ABCDA'B'C'D'.Tính góc giữa BD và (B'AC)

Những câu hỏi liên quan
Cho hình lập phương ABCDA'B'C'D' Tính góc giữa hai đường thẳng AC và A'B
Áp dụng định lí Pytago trong các tam giác vuông ta tính được:
\(AC=a\sqrt{2};AB'=a\sqrt{2};B'C=a\sqrt{2}\)
Do đó tam giác ACB’ là tam giác đều
\(\Rightarrow\left(\widehat{AC;AB'}\right)=\widehat{CAB'}=60^o\)
Đúng 1
Bình luận (0)
cho hình lập phương abcda'b'c'd'. số đo của góc giữa hai đường thẳng ab và dd' là
Góc giữa AB và DD' = góc giữa AB và AA' ( vì DD'=AA')
Nên bằng 90 độ
Đúng 0
Bình luận (0)
\(\widehat{\left(AB,DD'\right)}=\widehat{\left(AB,AA'\right)}=\widehat{BAA'}=90^o\) do DD'//AA'.
Đúng 0
Bình luận (0)
Cho hình lập phương ABCDA'B'C'D' chứng minh BD' vuông góc với mặt phẳng A'C'D
cho hình lăng trụ ABCDA'B'C'D' đáy là hình thoi cạnh A tâm O, góc ABC=120°. góc giữa AA' và đáy là 60°. A' cách đều A,B,D. Tính thể tích ABCDA'B'C'D'
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính góc giữa hai đường thẳng BD và AC
A . 60 0
B . 30 0
C . 45 0
D . 90 0
Đáp án D
Có hình chiếu của AC' xuống đáy là AC mà AC ⊥ BC nên AC'BD.
Đúng 0
Bình luận (0)
Cho hình lập phương ABCA A'B'C'D' có cạnh bằng a Tính góc giữa hai đường thẳng BD và AC
A. 60 0
B. 30 0
C. 45 0
D. 90 0
Đáp án D
Có hình chiếu của AC' xuống đáy là AC mà A C ⊥ B D nên A C ' ⊥ B D .
Đúng 0
Bình luận (0)
b1: cho hình hộp ABCDA'B'C'D' có tất cả các mặt đều là hinh fthoi cạnh a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC
b2: cho tứ diện ABCD có CD=z/2 AB. I,J,K lần lượt là trung điểm của BC,AC,BD. biết JK=5/6AB. tính góc giữa CD với Ị và AB
b1: cho hình hộp ABCDA'B'C'D' có tất cả các mặt đều là hinh fthoi cạnh a. góc BAA'= góc BAD = góc DAA' = 60 độ. tính độ dài AC
b2: cho tứ diện ABCD có CD=1/2 AB. I,J,K lần lượt là trung điểm của BC,AC,BD. biết JK=5/6AB. tính góc giữa CD với ỊJ và AB
Đúng 0
Bình luận (0)
cho hình hộp đứng ABCDA'B'C'D' , ABCD là hình vuông , O là tâm hình vuông , OA' =a , góc giữa OA' và (ABCD) là 60 độ . tính thể tính hình hộp
Cho hình lập phương
A
B
C
D
A
B
C
D
cạnh a. Tính thể tích V của khối tứ diện
A
B
C
D
. A.
V
a
3
3
B....
Đọc tiếp
Cho hình lập phương A B C D A ' B ' C ' D ' cạnh a. Tính thể tích V của khối tứ diện A B ' C ' D ' .
A. V = a 3 3
B. V = a 3 6
C. V = a 3 2
D. V = 2 a 3 12