Chọn B

Chọn A

MN = DE; MP= DF; NP = EF.

NMP = EDF

C

A

A

a: \(S_{DEF}=\dfrac{DE\cdot DF}{2}=\dfrac{DH\cdot FE}{2}\)

nên \(DE\cdot DF=DH\cdot FE\)

c: Xét ΔDHE vuông tại H có HN là đường cao

nên \(DN\cdot DE=DH^2\left(1\right)\)

XétΔDHF vuông tại H có HM là đường cao

nên \(DM\cdot DF=DH^2\left(2\right)\)

Từ(1) và (2) suy ra \(DN\cdot DE=DM\cdot DF\)

hay DN/DF=DM/DE

Xét ΔDNM vuông tại D và ΔDFE vuông tại D có

DN/DF=DM/DE

Do đó: ΔDNM\(\sim\)ΔDFE

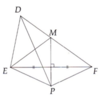
Do DE < DF nên M thuộc cạnh DF.

a) Có M thuộc đường trung trực của EF nên ME = MF

=> DM + ME = DM + MF = DF.

b) Vì P thuộc đường trung trực của EF nên PE = PF =>DP + PE = DP + PF.

Xét tam giác DEF: DP + PF > DF.

Vậy DE + PE > DF.

c) Từ ý a) và ý b) suy ra DP + PE > DM + ME.

Vậy chu vi tam giác DEP lớn hơn chu vi tam giác DEM.

a) \(EF=\sqrt{3^2+4^2}=5\)(cm)

\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{3\cdot4}{5}=\dfrac{12}{5}=2,4\left(cm\right)\)

b) \(EF=\sqrt{12^2+9^2}=15\left(cm\right)\)

\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{9\cdot12}{15}=\dfrac{108}{15}=7.2\left(cm\right)\)

c) \(EF=\sqrt{12^2+5^2}=13\left(cm\right)\)

\(DH=\dfrac{DE\cdot DF}{EF}=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\)

a: Xét ΔDEF có DI là phân giác

nên \(\dfrac{IE}{IF}=\dfrac{DE}{DF}\)

=>\(\dfrac{IE}{4,8}=\dfrac{10}{6}=\dfrac{5}{3}\)

=>IE=8(cm)

b: Xét ΔEDF có MI//DF

nên \(\dfrac{EM}{ED}=\dfrac{EI}{EF}\)

=>\(\dfrac{EM}{10}=\dfrac{8}{12.8}=\dfrac{5}{8}\)

=>\(EM=\dfrac{50}{8}=6,25\left(cm\right)\)

Ta có: ME+MD=DE

=>MD+6,25=10

=>MD=3,75(cm)

Xét ΔEDF có IM//DF

nên \(\dfrac{IM}{DF}=\dfrac{EI}{EF}\)

=>\(\dfrac{IM}{6}=\dfrac{8}{12,8}=\dfrac{5}{8}\)

=>\(IM=6\cdot\dfrac{5}{8}=3,75\left(cm\right)\)

c: Xét ΔEDF có MI//DF

nên \(\dfrac{ME}{MD}=\dfrac{EI}{IF}\)

mà \(\dfrac{EI}{IF}=\dfrac{DE}{DF}\)

nên \(\dfrac{ME}{MD}=\dfrac{DE}{DF}\)

a: Xét ΔDHE và ΔDHF có

DH chung

HE=HF

DE=DF

Do đó: ΔDHE=ΔDHF

b: Xét ΔDMH vuông tại M và ΔDNH vuông tại N có

DH chung

\(\widehat{MDH}=\widehat{NDH}\)

Do đó: ΔDMH=ΔDNH

Suy ra: DM=DN

a, Xét ΔDHE và ΔDHF có:

    DE = DF

    DH ( cạnh chung )

    HE = HF ( vì H là trung điểm của EF )

⇒ ΔDHE = ΔDHF ( C.C.C )

b, Xét ΔDMH vuông tại M và ΔDNH vuông tại N có :

DH (cạnh chung )

∠MDH = ∠NDH

⇒ ΔDMH=ΔDNH

⇒ DM=DN