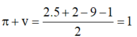Cách tính số liên kết π + vòng của C8H8.

Những câu hỏi liên quan
Trong công thức CxHyOzNt tổng số liên kết
π
và vòng là:
2
x
-
y
+
t
+
2
2
B. 2x-y +t+2.
2
x
-
y
-
t
+...
Đọc tiếp
Trong công thức CxHyOzNt tổng số liên kết π và vòng là:
2 x - y + t + 2 2
B. 2x-y +t+2.
2 x - y - t + 2 2
2 x - y + z + t + 2 2
Tổng số liên kết
π
và vòng ứng với công thức C5H9O2Cl là: A. 0. B. 1. C. 2. D. 3.
Đọc tiếp
Tổng số liên kết π và vòng ứng với công thức C5H9O2Cl là:
A. 0.
B. 1.
C. 2.
D. 3.
Tổng số liên kết
π
và vòng ứng với công thức C5H12O2 là: A. 0. B. 1. C. 2. D. 3.
Đọc tiếp
Tổng số liên kết π và vòng ứng với công thức C5H12O2 là:
A. 0.
B. 1.
C. 2.
D. 3.
Tổng số liên kết
π
và vòng trong phân tử axit benzoic là: A. 3. B. 4. C. 5. D. 6.
Đọc tiếp
Tổng số liên kết π và vòng trong phân tử axit benzoic là:
A. 3.
B. 4.
C. 5.
D. 6.
Tổng số liên kết π và vòng trong phân từ axit benzoic là
A. 3
B. 4
C. 5
D. 6
Một phân tử ADN dài 0,51um.tổng số nu loại G chiếm 20% tổng số nu.
1) khối lượng phân tử ADN
2) số vòng xoắn(chu kì xoắn) của phân tử.
3) tính tổng liên kết hóa trị.
4) tính tổng số liên kết hidro của phân tử ADN.
.
Có \(L=0,51\mu m=5100A^o\)
a) \(N=\dfrac{2L}{3,4}=\dfrac{2\cdot5100}{3,4}=3000\left(nu\right)\)
\(M=N\cdot300=3000\cdot300=900000\left(đvC\right)\)
b) \(C=\dfrac{N}{20}=\dfrac{3000}{20}=150\)(vòng xoắn)
c) Có số nu loại G chiếm 20% tổng số nu.
\(\Rightarrow G=3000\cdot20\%=600\left(nu\right)\)
Mà \(2A+2G=N\Rightarrow2\cdot A+2\cdot600=3000\Rightarrow A=900\left(nu\right)\)
Tổng số liên kết hóa trị: \(2N-2=2\cdot3000-2=5998\left(liênkết\right)\)
d) Số liên kết hidro phân tử ADN:
\(H=2A+3G=2\cdot900+3\cdot600=3600\left(liênkết\right)\)
Đúng 2
Bình luận (0)
Một gen(1 đoạn phân tử ADN) có tổng số nucleotit là 3000. Biết 3/2G: Tính a) Chiều dài của gen. b) Khối lượng gen. c) Số vòng xoắn. d) Số liên kết hóa trị. d) Số liên kết hidro.
a) Chiều dài của gen
\(L=\dfrac{N\times3,4}{2}=5100A^o\)
b) Khối lượng của gen
\(M=300N=9\times10^5\left(đvC\right)\)
c) Số vòng xoắn
\(C=\dfrac{N}{20}=150\left(ck\right)\)
Số liên kết hóa trị của gen
2N - 2 = 5998 (lk)
d) Thiếu dữ kiện
Đúng 2
Bình luận (0)
Tính số nucleotit,chiều dài,số liên kết hydro,số vòng xoắn
trong 1 phân tử ADN. tổng số nu loại A = 10% tổng số. biết khối lượng phân tử là 600000 Dvc. tính.
1) chiều dài phân tử ADN
2) số vòng xoắn(chu kì xoắn) của phân tử
3) tính tổng liên kết hóa trị
4) tính tổng số liên kết hidro của phân tử ADN
1. \(M=N\cdot300\Rightarrow N=\dfrac{M}{300}=\dfrac{60000}{300}=200\left(nu\right)\)
2. \(C=\dfrac{N}{20}=\dfrac{200}{20}=10\) (vòng xoắn)
3. Tổng liên kết hóa trị: \(2N-2=2\cdot200-2=398\left(nu\right)\)
4. Ta có: \(N_A=10\%N\Rightarrow N_A=20\left(nu\right)\)
Mà: \(2A+2G=200\Rightarrow2\cdot20+2\cdot G=200\Rightarrow G=80\left(nu\right)\)
Số liên kết hóa trị: \(H=2A+3G=2\cdot20+3\cdot80=280\left(liênkết\right)\)
Đúng 1
Bình luận (0)