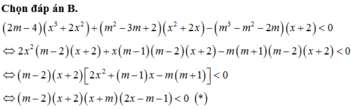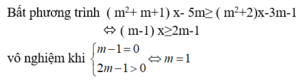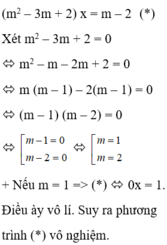Bất phương trình (m2 + 3m)x - m < 4 + 4x vô nghiệm khi nào ?

Những câu hỏi liên quan
Bất phương trình ( m 2 - 3 m ) x + m < 2 - 2 x vô nghiệm khi?
A. m ≠ 1
B. m ≠ 2
C. m = 2
D. m ∈ R
Bất phương trình tương đương: ( m 2 − 3 m + 2 ) x < 2 − m
Nếu m 2 − 3 m + 2 ≠ 0 ⇔ m ≠ 1 m ≠ 2 bất phương trình luôn có nghiệm.
Với m = 1 , bất phương trình trở thành 0 x < 1 (luôn đúng) nên bất phương trình có nghiệm đúng với mọi x ∈ ℝ .
Với m = 2 , bất phương trình ở thành 0 x < 0 (vô lí) nên bất phương trình vô nghiệm
Chọn đáp án C.
Đúng 0
Bình luận (0)
Với giá trị nào của m thì bất phương trình ( m 2 + m + 1)x - 5m ≥ ( m 2 + 2)x - 3m - 1 vô nghiệm ?
A. m = 1
B. m ≥ 1
C. m < 1
D. m ≤ 1
Chọn A.
Bất phương trình ( m 2 + m + 1)x - 5m ≥ ( m 2 + 2)x - 3m - 1 ⇔ (m - 1)x ≥ 2m - 1 vô nghiệm khi
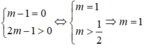
Đúng 0
Bình luận (0)
Giá trị nào của m thì bất phương trình ( m 2 + m + 1)x - 5m ≥ ( m 2 + 2)x - 3m - 1 vô nghiệm là:
A. m = 1
B. m ≥ 1
C. m < 1
D. m ≤ 1
Chọn A.
Bất phương trình ( m 2 + m + 1)x - 5m ≥ ( m 2 + 2)x - 3m - 1 ⇔ (m - 1)x ≥ 2m - 1 vô nghiệm khi
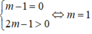
Đúng 0
Bình luận (0)
Gọi n là số các giá trị của tham số m để bất phương trình
(
2
m
-
4
)
(
x
3
+
2
x
2
)
+
(
m
2
-
3
m
+
2
)
-
(
m
3
–
m
2
-
2
m...
Đọc tiếp
Gọi n là số các giá trị của tham số m để bất phương trình ( 2 m - 4 ) ( x 3 + 2 x 2 ) + ( m 2 - 3 m + 2 ) - ( m 3 – m 2 - 2 m ) ( x + 2 ) < 0 vô nghiệm. Giá trị của n bằng
A. 5
B. 1
C. 4
D. 2
1.Bất phương trình (m2-3m)x+m<2-2x vô nghiệm khi:
a.m#1 b.m#2 c.m=2 d.=3
2.Gọi S là tập hợp tất cả các giá trị thực của tham số m để bất phương trình (m2-m)x +m<6x-2
GIUP MÌNH VỚI Ạ
Câu 2 bạn ghi thiếu đề
Câu 1:
\(\Leftrightarrow\left(m^2-3m\right)x+2x< 2-m\)
\(\Leftrightarrow\left(m^2-3m+2\right)x< 2-m\)
BPT đã cho vô nghiệm khi và chỉ khi:
\(\left\{{}\begin{matrix}m^2-3m+2=0\\2-m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\\m\ge2\end{matrix}\right.\) \(\Rightarrow m=2\)
Đúng 2
Bình luận (0)
Với giá trị nào của m thì bất phương trình
(
m
2
+
m
+
1
)
x
-
5
m
≥
(
m
2
+
2
)
x
-
3
m
-
1
vô nghiệm ? A. m 1 B. m 1 C. m 1 D. m ≤ 1
Đọc tiếp
Với giá trị nào của m thì bất phương trình ( m 2 + m + 1 ) x - 5 m ≥ ( m 2 + 2 ) x - 3 m - 1 vô nghiệm ?
A. m > 1
B. m = 1
C. m < 1
D. m ≤ 1
Với giá trị nào của m thì bất phương trình m 2 x + m - 1 < x vô nghiệm?
A. m = 1 và m = -1
B. m = 1
C. m = -1
D. m ∈ ∅
Chọn B.
Xét bất phương trình:
m 2 x + m - 1 < x ⇔ m 2 x - x + m - 1 < 0 ⇔ ( m 2 - 1)x < 1 - m (1)
Với m = 1, bất phương trình (1) trở thành: 0x < 0 ⇔ 0 < 0 (Vô lý) ⇒ Bất phương trình vô nghiệm.
Với m = -1 , bất phương trình (1) trở thành: 0x < 2 ⇔ 0 < 2 (luôn đúng) ⇒ Bất phương trình có vô số nghiệm.
Vậy bất phương trình m 2 x + m - 1 < x vô nghiệm khi m = 1.
Đúng 0
Bình luận (0)
Với giá trị nào của m thì bất phương trình m2x+ 4m - 3 < x + m2 vô nghiệm?
A. m = - 1
B. m= 1
C. ∅
D. m = -1 và m = 1
Cho phương trình ( m 2 – 3m + 2)x = m – 2, với m là tham số. Tìm m để phương trình vô số nghiệm
A. m = 1
B. m = 2
C. m = 0
D. m Є {1; 2}