Trong tứ giác ABCD, gọi A' ; B' ; C' ; D' theo thứ tự là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng bốn đường thẳng AA' ; BB' ; CC' ; DD' đồng quy .

Những câu hỏi liên quan
Cho tứ giác ABCD có AB AD, CB CD (ta gọi tứ giác ABCD trong trường hợp này là tứ giác có hình cánh diêu).a) Chứng minh AC là đường trung trực của BD.b) Tính
B
^
,
D
^
b
i
ế
t
A
^
100
O
,
C
^
...
Đọc tiếp
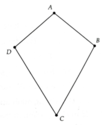
Cho tứ giác ABCD có AB = AD, CB = CD (ta gọi tứ giác ABCD trong trường hợp này là tứ giác có hình cánh diêu).
a) Chứng minh AC là đường trung trực của BD.
b) Tính B ^ , D ^ b i ế t A ^ = 100 O , C ^ = 60 O
a) HS tự chứng minh
b) Sử dụng tổng bốn góc trong tứ giác và chú ý B ^ = D ^
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có điểm O nằm trong tứ giác ABCD. Gọi S là diện tích của tứ giác ABCD
CMR: \(OA^2+OB^2+OC^2+OD^2\ge2S\)
Hạ CH vuông góc với OB tại H. Theo quan hệ đường xiên hình chiếu:
\(CH\le OC\Leftrightarrow CH.OB\le OC.OB\Leftrightarrow2.S_{BOC}\le OC.OB\)(Do \(S_{BOC}=\frac{CH.OB}{2}\))
Áp dụng BĐT Cauchy, ta có: \(OC.OB\le\frac{OC^2+OB^2}{2}\)
\(\Rightarrow2.S_{BOC}\le\frac{OC^2+OB^2}{2}\left(1\right)\). Chứng minh tương tự ta được:
\(2.S_{AOB}\le\frac{OA^2+OB^2}{2}\left(2\right);2.S_{DOC}\le\frac{OD^2+OC^2}{2}\left(3\right);2.S_{AOD}\le\frac{OA^2+OD^2}{2}\left(4\right)\)
Cộng (1); (2); (3) và (4) theo vế:
\(2.\left(S_{BOC}+S_{AOB}+S_{DOC}+S_{AOD}\right)\le\frac{2.\left(OA^2+OB^2+OC^2+OD^2\right)}{2}\)
\(\Rightarrow2S\le OA^2+OB^2+OC^2+OD^2\)=> ĐPCM.
Đúng 0
Bình luận (0)
\(2.S_{BOC}\le OC.OB\). Dấu "=" xảy ra <=> OC vuông góc với OB
\(OC.OB\le\frac{OC^2+OB^2}{2}\). Dấu "=" xảy ra <=> OC=OB
Suy ra \(2.S_{BOC}\le\frac{OC^2+OB^2}{2}\). Dấu "=" xảy ra <=> \(\Delta\)BOC vuông cân tại O
Tương tự với các tam giác AOB; AOD; DOC.
Vậy dấu "=" xảy ra <=> Tứ giác ABCD là hình vuông và O là tâm của hình vuông này.
Đúng 0
Bình luận (0)
tứ giác abcd có ac=a bd=b. gọi m là 1 điểm nằm trong tứ giác hỏi tổng khoảng cách từ M đến 4 đỉnh tứ giác có giá trị nhỏ nhất là bao nhiêu
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
Tứ giác ABCD có AC = a , BC =b .Gọi M là một điểm nằm trong tứ giác.Hỏi tổng khoảng cách từ M đến bốn đỉnh tứ giác có giá trị nhỏ nhất là bao nhiêu
cho tứ giác ABCD. Gọi M,N,P.Q lần lượt là trung điểm của AB,BC,CD,DA.
a)Tứ giác MNPQ là hình gì
b)Tìm điều kiện của tứ giác ABCD để tứ giác MNPQ là hình chữ nhật
a: Xét ΔABD có M,Q lần lượt là trung điểm của AB,AD
=>MQ là đường trung bình của ΔABD
=>MQ//BD và \(MQ=\frac{BD}{2}\)
Xét ΔCBD có
N,P lần lượt là trung điểm của CB,CD
=>NP là đường trung bình của ΔCBD
=>NP//BD và \(NP=\frac{BD}{2}\)
Ta có: MQ//BD
NP//BD
Do đó: MQ=NP
Ta có: \(MQ=\frac{BD}{2}\)
\(NP=\frac{BD}{2}\)
Do đó: MQ=NP
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
Do đó: MNPQ là hình bình hành
b: Xét ΔBAC có
M,N lần lượt là trung điểm của BA,BC
=>MN là đường trung bình của ΔBAC
=>MN//AC
Hình bình hành MNPQ trở thành hình chữ nhật thì MN⊥MQ
mà MN//AC
nên MQ⊥AC
Ta có: MQ⊥AC
MQ//BD
Do đó: BD⊥AC
Đúng 0
Bình luận (0)
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . gọi chu vi của tứ giác ABCD là PABCD . chứng minh
a) AC+BD>\(\dfrac{P_{ABCD}}{2}\)
b) Nếu AC<\(\dfrac{P_{ABCD}}{2}\) thì AC+BD<PABCD
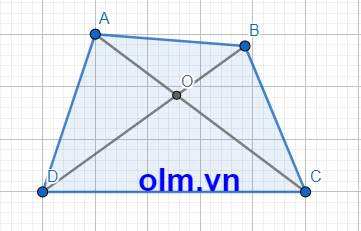
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)
Đúng 1
Bình luận (0)
Cho tứ giác ABCD và một điểm O ở bên trong tứ giác. gọi S là diện tích tứ giác ABCD. Chứng minh rằng : \(OA^2+OB^2+OC^2+OD^2\ge2S\)
dùng bất đẳng thức cauchy
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi M,N,P,Q thứ tự là trung điểm của AB,BC,CD,DA. a,CMR: Tứ giác MNPQ là hình bình hành b, So sáng chứ vi tứ giác MNPQ với tổng hai đường chéo của tứ giác ABCD
a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\)(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và \(NP=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành
Đúng 0
Bình luận (1)
b) ✱Xét Δ ABD có :
AM = BM ( gt )
AQ = DQ ( gt )
⇒ QM là đg trung bình của Δ ABD
⇒ MQ = 1/2 BD
✱Xét Δ BDC có :
BN = CN ( gt )
DP = PC ( gt )
⇒ NP là đg trung bình Δ BDC
⇒ NP = 1/2 BD
Ta có :
Chu vi tg MNPQ là:
MN + NP + PQ + QM ⇔ 1/2 AC + 1/2 BD + 1/2 AC + 1/2 BD
⇔ MN + NP + PQ + QM = AC + BD
Mà AC và BD là đg chéo của tg ABCD
⇒ Chu vi tg MNPQ = tổng 2 đg chéo tg ABCD
Đó , m ghi vô ii ko mai thầy chửi sấp mặt đấy !
Đúng 1
Bình luận (4)
Cho tứ giác ABCD,gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CD,DA
a,Tứ giác MNPQ là hình gì?Vì sao?
b, Tìm điều kiện của tứ giác ABCD để tứ giác MNPO là hình chữ nhật,hình thoi,hình vuông
c, Trong trường hợp tứ giác MNPQ là hình chữ nhật, tính diện tích hình chữ nhật MNPQ biết AC=20cm,BD=3/2 AC
Em cần gấp câu c ạ. EM sắp thi học kì r
a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Để mNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD
Để MNPQ là hình thoi thì MN=MQ
=>AC=BD
c: BD=3/2*AC=30cm
=>MQ=BD/2=15cm; MN=AC/2=10cm
SMNPQ=15*10=150cm2
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có
C
^
50
0
,
D
^
70
0
. Gọi E là giao điểm của các đường phân giác trong
A
^
,
B
^
. Số đó của
A
E
B
^
là: A. 300; ...
Đọc tiếp
Cho tứ giác ABCD có C ^ = 50 0 , D ^ = 70 0 . Gọi E là giao điểm của các đường phân giác trong A ^ , B ^ . Số đó của A E B ^ là:
A. 300;
B. 900;
C. 600;
D. 1200


















