ve tam giac ABC va một đường thang ra song song với BC cắt AB và AC lần lượt ở d và e. Viết các cặp góc bằng nhau , bù nhau giải thích vì sao(hk tinh hai goc doi dinh, hai góc kề bù)

Những câu hỏi liên quan
Mong mng giải đáp ạ
Vẽ tam giác ABC và một đường thẳng xy song song với BC cắt AB và AC lần lượt ở D và E. Viết các cặp góc bằng nhau, bù nhau . Giair thích vì sao. (kh tính 2 góc đối đỉnh, 2 góc kề bù)
Cảm ơn mng ạ :3
\(\widehat{ADE}=\widehat{ABC}\) (góc đồng vị)
\(\widehat{AED}=\widehat{ACB}\) (góc đồng vị)
\(\widehat{ABC}+\widehat{BDE}=180^o\) (hai góc trong cùng phía bù nhau)
\(\widehat{ACB}+\widehat{CED}=180^o\) (hai góc trong cùng phía bù nhau)
\(\widehat{ABC}=\widehat{BDx}\) (góc sole trong)
\(\widehat{ACB}=\widehat{CEy}\) (góc sole trong)
Đúng 0
Bình luận (0)
Vẽ tam giác ABC và một đường thẳng xy song song với BC cắt AB và AC lần lượt ở D và E.Viết các cặp góc bằng nhau và bù nhau.Giải thích vì sao( ko tính hai góc đối đỉnh,kề bù)
Cho tam giác ABC.Từ A vẽ AD vuông góc BC tại D,từ B vẽ BE vuông góc AC,từ C vẽ CF vuông góc AB.Nhận xét gì về 3 đường thẳng AD,BE,CF
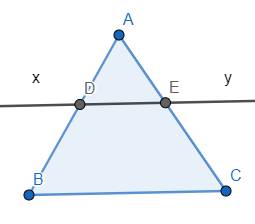
Dễ dàng thấy được \(\widehat{ABC}=\widehat{ADE}\) và \(\widehat{ACB}=\widehat{AED}\) (vì với mỗi cặp thì hai góc của cặp đó là hai góc so le trong)
Vì \(\widehat{ADE}\) và \(\widehat{BDE}\) là hai góc kề bù nên \(\widehat{ADE}+\widehat{BDE}=180^o\)
Mà \(\widehat{ABC}=\widehat{ADE}\) nên \(\widehat{ABC}+\widehat{BDE}=180^o\), suy ra \(\widehat{ABC}\) và \(\widehat{BDE}\) là hai góc bù nhau.
Suy luận tương tự như trên, ta được \(\widehat{ACB}\) và \(\widehat{CED}\) là hai góc bù nhau.
Đúng 1
Bình luận (0)
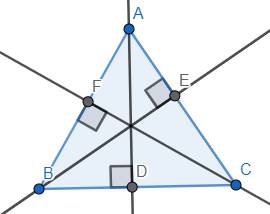
Nhận xét: AD, BE và CF là các đường cao, chúng đồng quy tại một điểm.
Đúng 1
Bình luận (0)
Vẽ tam giác ABC và một đường thẳng d song song với BC cắt AB và AD lần lượt ở D và E. Viết các cặp góc bằng nhau, bù nhau. Giải thích vì sao ?
từ điểm m ở giữa cạnh ab của tam giác abc ta kẻ hai tia lần lượt song song với ac và bc , cắt ac ở n , bc ở l a, nêu các cặp tam giác đồng dạng b, đối vs mỗi cặp viết ra góc bằng nhau và các tỉ số tương ứng
a: Xét ΔAMI và ΔABC có
góc AMI=góc ABC
góc A chung
=>ΔAMI đồng dạng với ΔABC
Xét ΔBMN và ΔBAC có
góc B chung
góc BMN=góc BAC
=>ΔBMN đồng dạng với ΔBAC
=>ΔMBN đồng dạng với ΔABC
=>ΔMBN đồng dạng với ΔAMI
b: ΔAMI đồng dạng với ΔABC
=>AM/AB=AI/AC=MI/BC và góc AMI=góc ABC; góc AIM=góc ACB
ΔMBN đồng dạng với ΔABC
=>MB/BA=BN/BC=MN/AC và góc BMN=góc BAC; góc BNM=góc BCA
ΔAMI đồng dạng với ΔMBN
=>AM/MB=MI/BN=AI/MN và góc MAI=góc MBN; góc AMI=góc MBN; góc AIM=góc MNB
Đúng 0
Bình luận (0)
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
a) Tìm các hình thang trong hình vẽ
b)chứng minh rằng hình thang BDEC là một cạnh đáy bằng tổng hai cạnh bên
b: Xét ΔDBI có
\(\widehat{DBI}=\widehat{DIB}\)
nên ΔDBI cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=DB+EC
Vậy: BDEC là hình thang có một cạnh đáy bằng tổng hai cạnh bên
Đúng 0
Bình luận (0)
Bài 1 : Cho tam giác ABC, lấy điểm E nằm trên cạnh AB. Qua E vẽ đường thẳng d song song với BC, d cắt AC tai F.
a, Kể tên các cặp góc bằng nhau của hai tam giác AEF và BAC. Giải thích?
b, Nếu cho .Tính góc AEF = 50độ , AFE = 60độ Tính góc A
AI GIÚP VỚI MÌNH CẦN LUÔN .
Cho tam giác ABC cân ở A có AI là phân giác và CH là đường cao.a. Tính BH nếu biết AB10cm, BC6cm.b. Đường thẳng qua I song song với AB cắt AC ở K. Đường thẳng qua K song song với BC cắt AB ở J. Chứng minh HIKJ là hình thang cân.c. Chứng minh BH.CKBI^2 và tam giác BIH đồng dạng với tam giác IKHd. Chứng minh IK.HB+KC.IH HK.BIe. Gọi O là giao điểm của IJ và HK, AO cắt BC ở E. Dựng góc BCx kề góc BCA sao cho góc BCx bằng góc BAE. Hai tia AE và Cx cắt nhau ở D. Chứng minh tam giác BED đồng dạng với...
Đọc tiếp
Cho tam giác ABC cân ở A có AI là phân giác và CH là đường cao.
a. Tính BH nếu biết AB=10cm, BC=6cm.
b. Đường thẳng qua I song song với AB cắt AC ở K. Đường thẳng qua K song song với BC cắt AB ở J. Chứng minh HIKJ là hình thang cân.
c. Chứng minh BH.CK=BI^2 và tam giác BIH đồng dạng với tam giác IKH
d. Chứng minh IK.HB+KC.IH > HK.BI
e. Gọi O là giao điểm của IJ và HK, AO cắt BC ở E. Dựng góc BCx kề góc BCA sao cho góc BCx bằng góc BAE. Hai tia AE và Cx cắt nhau ở D. Chứng minh tam giác BED đồng dạng với tam giác AEC và AC^2 = AD.AE
g. Chứng minh AD^2=BD.CD + AB^2
Cho tam giác ABC, góc CAB 90oa, Vẽ AH vuông góc BC tại Hb,Qua H lần lượt vẽ HD vuông góc với AC tại D và HE vuông góc HD (E thuộc cạnh AB ). TÌm và giải thích hai cặp đường thẳng song song có trên hình vẽc, Tìm( có giải thích ) các cặp óc tương ứng bằng nhau của hai tam giác BEH và HDC d,Tìm các cặp góc có đỉnh H bằng nhaue, So sánh hai góc BAH và BCA------------------------------------------------------------------hết---------------------------------------------------------------MÌNH ĐANG CẦN G...
Đọc tiếp
Cho tam giác ABC, góc CAB= 90o
a, Vẽ AH vuông góc BC tại H
b,Qua H lần lượt vẽ HD vuông góc với AC tại D và HE vuông góc HD (E thuộc cạnh AB ). TÌm và giải thích hai cặp đường thẳng song song có trên hình vẽ
c, Tìm( có giải thích ) các cặp óc tương ứng bằng nhau của hai tam giác BEH và HDC
d,Tìm các cặp góc có đỉnh H bằng nhau
e, So sánh hai góc BAH và BCA
------------------------------------------------------------------hết---------------------------------------------------------------
MÌNH ĐANG CẦN GẤP, GIẢI CỤ THỂ GIÚP MÌNH NHA
Bạn tự vẽ hình nhé
Xét tứ giác EHDA có 3 góc vuông ( CAB = HDA = EHD = 90 độ ) nên AHDA là hình chữ nhật
b) HE song song với AC do cùng vuông với AB
HD song song với AB do cùng vuông với AC
c) Do EHDA là hình chữ nhật nên góc HEA = 90 độ và góc HDA = 90 độ
suy ra góc BEH = góc HDC = 90 độ
Do EH song song với AC nên góc BHE = góc C ( hai góc đồng vị )
Do HD song song với AB nên gocsDHC = góc C ( hai góc đồng vị )
d) Ta thấy: góc BHE + góc EHA = góc BHA = 90 độ ( do H vuông góc với BC )
góc DHA + góc EHA = góc EHD = 90 độ ( do HE vuông góc HD )
suy ra góc BHE = góc DHA
Tương tự ta có góc EHA = góc DHC ( cùng phụ với góc AHD )
e) Ta thấy góc BAH + góc HAC = 90 độ
góc ACB + góc HAC = 180 độ - góc AHC = 90 độ
Suy ra góc BAH = góc ACB
Đây là lời giải chi tiết đó bạn
Đúng 1
Bình luận (0)
Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt các cạnh AB và AC ở D và E. Chứng minh rằng hình thang BDEC có một đáy bằng tổng hai cạnh bên.
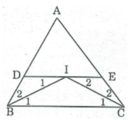
DE // BC (theo cách vẽ)
⇒ ∠ I 1 = ∠ B 1 (hai góc so le trong)
Mà ∠ B 1 = ∠ B 2 (gt)
Suy ra: ∠ I 1 = ∠ B 2
Do đó: ∆ BDI cân tại D ⇒ DI = DB (1)
Ta có: ∠ I 2 = ∠ C 1 (so le trong)
∠ C 1 = ∠ C 2 (gt)
Suy ra: ∠ I 2 = ∠ C 2 do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2), (3) suy ra: DE = BD + CE
Đúng 0
Bình luận (0)


















