Tập xác định: D = R.

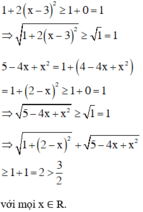
Do đó BPT 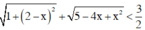 vô nghiệm.

a: 3x=81

nên x=27

b: \(5\cdot4^x=80\)

\(\Leftrightarrow4^x=16\)

hay x=2

c: \(2^x=4^5:4^3\)

\(\Leftrightarrow2^x=2^4\)

hay x=4

yggucbsgfuyvfbsudy

????????

a) Ta có :  2 x : 2 2 = 2 5  nên x = 7.

b) Ta có:  3 x : 3 2 = 3 5  nên x = 7.

c) Ta có :  4 4 : 4 x = 4 2  nên x = 2.

d) Ta có :  5 x : 5 2 = 5 2  nên x = 4,

e) Ta có:  5 x + 1 : 5 = 5 4  nên x = 4.

f) Ta có :  4 2 x - 1 : 4 = 4 2  nên x = 2

a,  \(\frac{\left(5-2x\right)}{3}=\frac{\left(4x-1\right)}{-5}\)

\(\Leftrightarrow-5(5-2x)=3\left(4x-1\right)\)

\(\Leftrightarrow10x-25=12x-3\)

\(\Leftrightarrow10x-12x=25-3\)

\(\Leftrightarrow-2x=22\)

\(\Leftrightarrow x=-11\)

b,  \(\frac{\left(12-3x\right)}{32}=\frac{6}{\left(4-x\right)}\)

\(\Leftrightarrow\frac{3\left(4-x\right)}{32}=\frac{6}{\left(4-x\right)}\)

\(\Leftrightarrow3(4-x)\left(4-x\right)=32.6\)

\(\Leftrightarrow(4-x)\left(4-x\right)=32.2\)

\(\Leftrightarrow(4-x)^2=64\)

\(\Leftrightarrow\orbr{\begin{cases}4-x=8\\4-x=-8\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=12\end{cases}}\)

c,  \(\frac{\left(10-2x\right)}{6}=\frac{27}{\left(5-x\right)}\)

\(\Leftrightarrow\frac{2\left(5-x\right)}{6}=\frac{27}{\left(5-x\right)}\)

\(\Leftrightarrow2(5-x)\left(5-x\right)=27.6\)

\(\Leftrightarrow(5-x)\left(5-x\right)=27.3\)

\(\Leftrightarrow(5-x)^2=81\)

\(\Leftrightarrow\orbr{\begin{cases}5-x=9\\5-x=-9\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=14\end{cases}}\)

a, \(\frac{5-2x}{3}=\frac{4x-1}{-5}\Leftrightarrow-25+10x=12x-3\Leftrightarrow-22-2x=0\Leftrightarrow x=-11\)

b, \(\frac{12-3x}{32}=\frac{6}{4-x}\Leftrightarrow\frac{12-3x}{32}=\frac{18}{12-3x}\)

\(\Leftrightarrow\left(12-3x\right)^2=576\Leftrightarrow12-3x=\pm2\)\(\Leftrightarrow\orbr{\begin{cases}x=\frac{10}{3}\\x=\frac{14}{3}\end{cases}}\)

c, \(\frac{10-2x}{6}=\frac{27}{5-x}\Leftrightarrow\frac{10-2x}{6}=\frac{54}{10-2x}\)

\(\Leftrightarrow\left(10-2x\right)^2=324\Leftrightarrow10-2x=\pm18\)\(\Leftrightarrow\orbr{\begin{cases}x=14\\x=-4\end{cases}}\)

\(\frac{5-2x}{3}=\frac{4x-1}{-5}\)

=> -5(5 - 2x) = 3(4x - 1)

=> -25 + 10x = 12x - 3

=> -25 + 10x - 12x +3  = 0

=> (-25 + 3) + (10x - 12x) = 0

=> -22 - 2x = 0

=> 2x = -22

=> x = -11

\(\frac{12-3x}{32}=\frac{6}{4-x}\)

=> (12 - 3x)(4 - x) = 32.6

=> 12(4 - x) - 3x(4 - x) = 192

=> 48 - 12x - 12x + 3x² = 192

=> 48 - 24x + 3x² = 192

=> 3(x² - 8x + 16) = 192

=> x² - 8x + 16 = 64

=>  x² - 4x - 4x + 16 = 64

=> x(x - 4) - 4(x - 4) = 64

=> (x - 4)² = 64

=> (x - 4)² = (\(\pm\)8)²

=> \(\orbr{\begin{cases}x-4=8\\x-4=-8\end{cases}}\Rightarrow\orbr{\begin{cases}x=12\\x=-4\end{cases}}\)

\(\frac{10-2x}{6}=\frac{27}{5-x}\)

=> (10 - 2x)(5 - x) = 27.6

=> 10(5 - x) - 2x(5 - x) = 162

=> 50 - 10x - 10x + 2x² = 162

=> 50 - 20x + 2x² = 162

=> 2(x² - 10x + 25) = 162

=> x² - 10x + 25 = 81

=> x² - 5x - 5x + 25 = 81

=> x(x - 5) - 5(x - 5) = 81

=> (x - 5)² = 81

=> (x - 5)² = (\(\pm\)9)²

=> \(\orbr{\begin{cases}x-5=9\\x-5=-9\end{cases}}\Rightarrow\orbr{\begin{cases}x=14\\x=-4\end{cases}}\)

ai giupws với

1) \(4x=7y\Leftrightarrow\dfrac{x}{7}=\dfrac{y}{4}\Rightarrow\dfrac{x^2}{49}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{49+16}=\dfrac{260}{65}=4\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2=4.49=196\\y^2=4.16=64\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=14,y=8\\x=-14,y=-8\end{matrix}\right.\) (vì \(\dfrac{x}{7}=\dfrac{y}{4}\) nên \(x,y\) cùng dấu) 

2) \(2^{x-1}+5.2^{x-2}=\dfrac{7}{32}\)

\(\Leftrightarrow2^{x-1}+\dfrac{5}{2}.2^{x-1}=\dfrac{7}{32}\)

\(\Leftrightarrow2^{x-1}=\dfrac{1}{16}=2^{-4}\)

\(\Leftrightarrow x-1=-4\)

\(\Leftrightarrow x=-3\)

3) \(\left|x+5\right|+\left(3y-4\right)^{2016}=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+5=0\\3y-4=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=\dfrac{4}{3}\end{matrix}\right.\)