Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD.chứng minh rằng CA là tia phân giác của góc C

Những câu hỏi liên quan
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C.
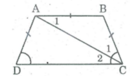
Ta có:
AB = AD (gt)
AD = BC (tính chất hình thang cân)
⇒ AB = BC do đó ΔABC cân tại B
⇒ ∠ BAC = ∠ BCA (tính chất tam giác cân) (*)
ABCD là hình thang có đáy là AB nên AB // CD
∠ BAC = ∠ DCA (hai góc so le trong) (**)
Từ (*) và (**) suy ra: ∠ BCA = ∠ DCA (cùng bằng ∠ BAC)
Vậy CA là tia phân giác của ∠ BCD.
Đúng 1
Bình luận (0)
Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C ?
Ta có: \(AB = AD\)
Mà \(AD = BC\) (ABCD là hình thang cân)
\(\Rightarrow AB=BC\)
Nối A và C
Ta có: \(AB=BC\Rightarrow\Delta ABC\) là \(\Delta\) cân \(\Rightarrow\widehat{BAC}=\widehat{BCA}\) (1)
Ta lại có: AB // CD (ABCD là hình tang cân)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\) ( cặp góc so le trong) (2)
Từ (1) và (2) \(\Rightarrow\widehat{BCA}=\widehat{ACD}\Rightarrow CA\) là phân giác của \(\widehat{C}\) (ĐPCM)
Đúng 0
Bình luận (0)
Bài 1: CHo hình thang ABCD có cạnh đáy nhỏ AB bằng cạnh bên AD.Chứng minh CA là phân giác góc C.
Bài 1: CHo hình thang ABCD có cạnh đáy nhỏ AB bằng cạnh bên AD.Chứng minh CA là phân giác góc C
CHO HÌNH THANG CÂN ABCD CÓ ĐÁY NHỎ AB BẰNG CẠNH BÊN AD.CHỨNG MINH:CA LÀ PHÂN GIÁC CỦA GÓC C
bn làm đúng, nhưng trình bày chưa sắc nét, làm dc như bn là quí lắm rùi,mk đúng cho bn
Đúng 0
Bình luận (0)
Vì ABCD là hình thang cân(gt)
=>AD=BC mà AD=AB(gt)
=>BC=AB=> tam giác ABC cân tại B(Đlí)
=>góc BAC = góc BCA (Đlí) mà góc BAC = góc ACD(AB//CD)
=>góc BCA = gócACD
=> ac là phân giác của gócC
Đúng 0
Bình luận (0)
: Hình thang cân ABCD, đáy nhỏ AB bằng cạnh bên AD. Chứng minh CA là tia phân giác góc C.
Ta có: AB=AD
mà AD=BC
nên BA=BC
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{BCA}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
Đúng 1
Bình luận (0)
bài 1: Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD.Chứng minh rằng CA là tia phân giác của góc Cbài 2: Tứ giác ABCD có ABBCAD , góc A 110 : C70a) DB là tia phân giác của góc Db)ABCD là Hình thang cânBài 3Cho tam giác ABC cân tại A . Lấy điểm D trên cạnh AB , điểm e trên cạnh AC sao cho ADAEa)Tứ giác BDCE là Hình gì ? Vì sao ?b) CÁc điểm D,E ở vị trí nào thì BDDEECMong các bạn nhanh giùm mkMình cần gấp!!!
Đọc tiếp
bài 1: Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD.Chứng minh rằng CA là tia phân giác của góc C
bài 2: Tứ giác ABCD có AB=BC=AD , góc A =110 : C=70
a) DB là tia phân giác của góc D
b)ABCD là Hình thang cân
Bài 3Cho tam giác ABC cân tại A . Lấy điểm D trên cạnh AB , điểm e trên cạnh AC sao cho AD=AE
a)Tứ giác BDCE là Hình gì ? Vì sao ?
b) CÁc điểm D,E ở vị trí nào thì BD=DE=EC
Mong các bạn nhanh giùm mk
Mình cần gấp!!!
Theo bài ra ta có tứ giác ANCD là hình thang cân
=> AD = BC
Mà AB = AD
=> AD = BC = AB
=> tam giác ABC có AB = Bc=> ABC là tam giác cân
=> góc BAC = góc BCA (1)
Vì AB//CD => góc BAC = góc ACD (2)
Từ (1) và (2)
=> góc BCA = góc ACD
=> AC là đường phân giác của góc C
=> đpcm
2) a) Kẻ BN vuông AD , BM vuông CD
Xét tam giác vuông BNA và BMD ta có :
AB = BC ; góc BNA = \(180^o-\widehat{BAD}=70^o\)nên góc BAN = BCD = \(70^o\)
\(\Rightarrow\)tam giác BMD = tam giác BND ( cạnh huyền - góc nhọn )
\(\Rightarrow\)\(BN=BM\Rightarrow BD\)là tia phân giác của góc D
b) Nối B với D do AB = AD nên tam giác ABD cân tại A khi đó góc ADB = ( \(180^o-110^o\)) : 2= \(35^o\)
\(\Rightarrow\widehat{ADC}=70^o\)
do góc ADC + góc BAD = \(180^o\Rightarrow\)AB// CD
Và góc BCD = góc ADC= \(70^o\)
Suy ra ABC là hình thang cân
Đúng 0
Bình luận (0)
hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C
mình cần ngay các bạn giúp mình với nhé !!!!!
Giai thuong cho cuoc thi nhanh tay nhất,phần thưởng là 3 cái tick ,mời các bạn cùng giải bài này
Hình thang ABCD có đáy nhỏ AB bằng cạnh bên AD.Chứng minh rằng CA là tia phân giác của góc C
















