a) chứng minh: A'B'C' đồng dạng D'E'F'
b) chứng minh: B'C'.D'F'=A'C'.E'F'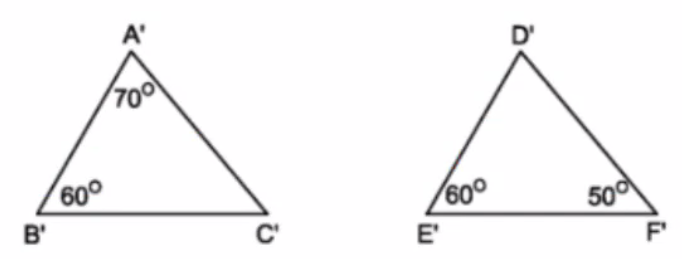

Những câu hỏi liên quan
a) Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', AC > A'C'. Không sử dụng định lí Pitago, chứng minh rằng BC > B'C'
b) Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', BC > B'C'. Không sử dụng định lí Pitago, chứng minh rằng AC > A'C'
a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.
Đúng 0
Bình luận (0)
Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', AC > A'C'. Không sử dụng định lý Pitago, chứng minh rằng BC > B'C'
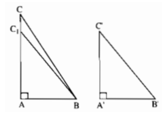
Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′. Ta có tam giác vuông ABC1 bằng tam giác vuông A'B'C', suy ra B′C′=BC1. Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1. Vì AC > AC1 nên BC > BC1. Suy ra BC > B'C'.
Đúng 0
Bình luận (0)
Hai tam giác ABC, A'B'C' vuông tại A và A' có AB = A'B', BC > B'C'.
Không sử dụng định lý Pytago, chứng minh rằng AC > A'C'
Dùng phản chứng:
- Giả sử AC < A'C'. Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC = A'C'. Khi đó ta có ΔABC = ΔA'B'C' (c.g.c). Suy ra BC = B'C'.
Điều này cũng không đúng với giả thiết BC > B'C'. Vậy ta phải có AC > A'C'.
(Nếu sử dụng định lý Pytago thì có thể giải bài toán sau)
Trong tam giác vuông ABC có BC 2= AB 2+ AC 2 (1)
Trong tam giác vuông A'B'C' có B'C' 2= A'B' 2+ A'C' 2 (2)
Theo giả thiết AB = A'B' nên từ (1) và (2) ta có:
- Nếu AC > A'C' thì AC 2 > A'C' 2, suy ra BC 2 > B'C' 2 hay BC > B'C'
- Nếu BC > B'C' thì BC 2 > B'C' 2, suy ra AC 2 > A'C' 2 hay AC > A'C'.
Đúng 0
Bình luận (0)
Cho tam giác ABC và tam giác A'B'C' có AB =A'B' , AC =A'C'.M thuộc BC sao cho MC = MB , M' thuộc B'C' sao cho M'C' = M'B' và AM = A'M' . Chứng minh : tam giác ABC = A'B'C'
Xét tam giác ABC và tam giác A'B'C' có:
AC=A'C(gt)
AB=A'B'(gt)
AM:cạnh chung <1>
A'M':cạnh chung <2>
Từ <1>và<2> có;AM=A'M'(vì đều là cạnh chung)
Vậy tam giác ABC =tam giác A'B'C'(c-c-c)
Cho tam giác ABC và tam giác A'B'C' có AB =A'B' , AC =A'C'.M thuộc BC sao cho MC = MB , M' thuộc B'C' sao cho M'C' = M'B' và AM = A'M' . Chứng minh : tam giác ABC = A'B'C'
Cho tam giác ABC và tam giác A'B'C' có AB=A'B', AC=A'C'. M thuộc BC sao cho MC=MB, M' thuộc B'C' sao cho M'C' =M'B' và AM=A'M'.Chứng minh tam giác ABC= tam giác A'B'C'
cho tam giác ABC , tam giác A'B'C' có gốc BAC+góc B'A'C' = 180 độ. AB=A'B' , AC=A'C' . M là trung điểm của BC . chứng minh AM=1/2 B'C'
cho tam giác ABC , tam giác A'B'C' CÓ GÓC BAC + góc B'C'A = 180 độ . AB=A'B' , AC=A'C'. M la trung diem cua BC . CHỨNG MINH AM=1/2 B'C'
Cho tam giác ABC và tam giác A'B'C' có AB=A'B', AC = A'C' ; góc A= A'( vẽ hình hộ mk thôi)
a, so sánh tam giác ABC và A'B'C'
b, trên các cạnh AB và A'B' lấy AM =A'M'
Chứng minh tam giác AMC =A'M'C'
c, Chứng minh BM=B'M'
d. Trên các cạnh BC và B'C' lấy BE = B'E'
Chứng minh tam giác MBE = M'B'E'
Cho \(\Delta\)ABC và \(\Delta\)A'B'C'. Vẽ BH\(\perp\)AC; B'H'\(\perp\)A'C'. Cho biết AB = A'B'; AC = A'C'. Chứng minh BC = B'C'
















