Cho tam giác ABC nhọn có đường cao là BD và CE cắt nhau tại I .CMR góc BIC bù với góc A

Những câu hỏi liên quan
Bài 1: Cho tam giác ABC nhọn có 2 đường cao AH và BD. chứng minh CAH=CBD
Bài 2: Cho tam giác ABC nhọn có 2 đường cao AH và BD cắt nhau ở I. Giả sử^C=60. Tính BIH
Bài 3: Cho tam giác ABC nhọn có 2 đường cao BD và CE cắt nhau ở I. BIC kề bù với góc nào? C/M BIC bù với góc A.
Vẽ hình và giải giúp mình với.
Cho tam giác ABC có ba góc nhọn, các đường cao BD, CE cắt nhau tại H.
a, CMR: tam giác ABD đồng dạng với tam giác ACE
b, CMR: BH.HD = CH.HE
c, CRM: góc ADE = góc ABC
d, Đường thẳng vuông góc với AB tại B, đường thẳng vuông góc với AC tại C, cắt nhau tại M. O là trung điểm BC, I là trung điểm AM. So sánh Sahm và Siom
a) Có góc A chung và 2 góc vuông => ĐPCM
b) Xét EHB và DHC có:
2 góc vuông và 2 góc đối đỉnh EHB và DHC
=> EHB đồng dạng với DHC
=>BH/CH=EH/DH
=>BH.DH=EH.CH
c)Từ câu a ta suy ra được tỉ số : AB/AC=AD/AE
và có góc A chung .
Từ đó suy ra: ADE đồng dạng với ABC
=> góc ADE= góc ABC
d) Ta có IO là đường trung bình ( tự chứng minh )
=> IO//AH => AHM đồng dạng với IOM
Tỉ số cạnh = AM/IM =2 ( do là đường trung bình )
Tỉ số diện tích của AHM so với IOM là 22=4
Vậy SAHM=4.SIOM
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có hai đường cao AH và BD cắt nhau ở I . Góc BIC kề bù với gó nào ? Chứng minh góc BIC bù với góc A
VẼ HÌNH GIÙM MÌNH NHÁ CÁC BẠN !!!!!!!!
mình ko biết vẽ à nhưng mình giải được cau hoi nay đó
Cho tam giác ABC có góc A=60, các đường phân BD và Ce cắt nhau tại I. Qua I kẻ đường thẳng vuông góc với BD, cắt BC ở F. CMR:
a/ E và F đối xứng nhau qua BD
b/ IF là tia phân giác góc BIC
c/ D và F đối xúng nhau qua IC
a) xét tg BEF có: BD là pg của ^B (gt) và EF vg vs BD (gt)
=> tg BEF cân tại B=> BD cx là đg trung trực ứng vs cạnh EF => E đx vs F qua BD
b)ta có: ^ BAC +^ ABC +^ACB=180( t/c tổng các goác trong tg)
=>60+ 2 ^IBC +2.^ICB=180 (vì ^ BAC=60 )
=> ^IBC+^ICB=60
xét tg IBC có: ^BIC +^ICB +^IBC =180 (t/c tổng các góc trong tg)
=> ^BIC= 120 (vì ^IBC +^ICB =60)
Mà ^BIC +\(^{\widehat{I}_1}\)=180 (vì 2 góc này bù nhau) =>\(^{\widehat{I}_1}\) =60 (vì ^BIC=120)
^BIC +\(\widehat{I_4}\)=180(vì.........................)=>\(\widehat{I_4}\)=60
=> \(^{\widehat{I}_1}\)= \(\widehat{I_2}\)=60 (vì 2 góc này đối xứng vs nhau)
và \(\widehat{I_4}\) = \(\widehat{I_3}\)=60(vì ...................................)
=>\(\widehat{I_2}\) =\(\widehat{I_3}\) =60 => IF là tia pg của ^BIC
c)xét tg IDC và tg IFC có: \(\widehat{I_4}\)= \(\widehat{I_3}\) (=60) ; IC chung ; ^DCI=^FCI (vì IC là pg của ^C)
=>tg IDC =tg IFC (g.c.g)
=> ID=IF và DC=FC => IC là đg trung trực của DF => D đx vs F qua IC
Đúng 0
Bình luận (0)
.sai rồi nha bạn góc I3 không bằng I4 được vì chưa chứng minh đối xứng thì ko thể bằng nhau được nha bạn😊
Đúng 0
Bình luận (0)
nguoi ta dung roi ko tin toi CM nguoc cho ong xem
Cho tam giác ABC có góc A=60, các đường phân BD và Ce cắt nhau tại I. Qua I kẻ đường thẳng vuông góc với BD, cắt BC ở F. CMR:
a/ E và F đối xứng nhau qua BD
b/ IF là tia phaan giác góc BIC
c/ D và F đối xúng nhau qua IC
Cho tam giác ABC có 3 góc nhọn , các đường cao BD và CE cắt nhau tại H
a. CMR: tam giác ABD đồng dạng với tam giác ACE
b. CMR: HB.HD=HC.HE
c.Cm: GÓC ADE= GÓC ABC
vẽ hình
a xét tam giác ABD và tam giác ACE có :
chung góc BAC
góc BDA = góc CEA = 90 độ
=> tam giác ABD đồng dạng tam giác ACE (g.g)
b, xét tam giác EHB và tam giác DHC có
góc BDC = góc CFB = 90 độ
góc BHF = góc DHC ( đối đỉnh )
=> tam giác EHB đồng dạng với tam giác DHC (g.g)
=> \(\frac{HB}{HC}=\frac{HE}{HD}\)
=> HD . HB = HE . HC ( đpcm )
c, vì tam giác ABD đồng dạng với tam giác ACE ( câu a)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\) => \(\frac{AE}{AC}=\frac{AD}{AB}\)
xét tam giác ADE và tam giác ABC có
chung góc BAC
\(\frac{AE}{AC}=\frac{AD}{AB}\)
=> tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
=> góc ADE = góc ABC ( đpcm)
Đúng 0
Bình luận (0)
cho tam giác abc có Â=60 độ, phân giác BD va CE cắt nhau tại I. qua E vẽ đường vuông góc với BD cắt BC ở F. CMR:
a) IF là phân giác góc BIC
b) D và F đối xứng qua IC
cho tam giác ABC , p/g BD và CE cắt nhau tại I. Qua E kẻ đường vuông góc với BD cắt BC tại F
a) CMR: E đối xứng với F qua BD
b) CMR: IF là phân giác của góc BIC
c) D và F đối xứng qua IC
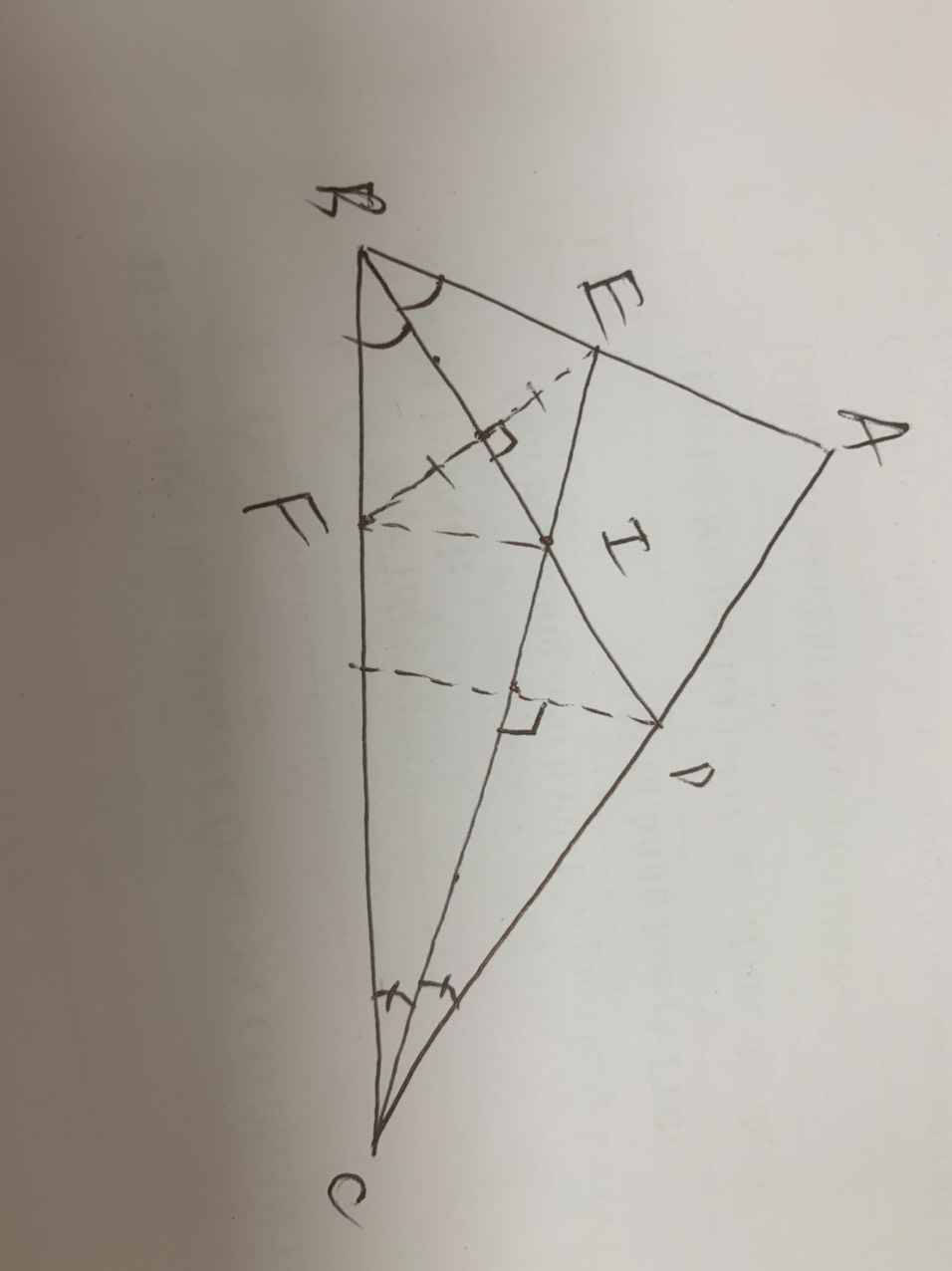 Với đề bài cho như bạn viết thì câu a thì chứng minh đúng được. Còn câu b thì IF không thể là phân giác của góc BCI được. Câu c là F không thể đối xứng được D qua CI (hình vẽ minh hoạ, luôn tồn tại điểm K trên BC khác điển F)
Với đề bài cho như bạn viết thì câu a thì chứng minh đúng được. Còn câu b thì IF không thể là phân giác của góc BCI được. Câu c là F không thể đối xứng được D qua CI (hình vẽ minh hoạ, luôn tồn tại điểm K trên BC khác điển F)
Đúng 0
Bình luận (1)
Cho tam giác ABC có các góc đều nhọn. Các đường cao BD và CE cắt nhau tại H. Chứng minh tam giác ABD đồng dạng tam giác ACECho tam giác ABC có các góc đều nhọn. Các đường cao BD và CE cắt nhau tại H.a) CM: Tam giác ABD đồng dạng tam giác ACE.b) CM: HB.HDHC.HEc) Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc AMCgóc ANB90 độ. CMR: AMAN.
Đọc tiếp
Cho tam giác ABC có các góc đều nhọn. Các đường cao BD và CE cắt nhau tại H. Chứng minh tam giác ABD đồng dạng tam giác ACECho tam giác ABC có các góc đều nhọn. Các đường cao BD và CE cắt nhau tại H.
a) CM: Tam giác ABD đồng dạng tam giác ACE.
b) CM: HB.HD=HC.HE
c) Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc AMC=góc ANB=90 độ. CMR: AM=AN.
a) CM: Tam giác ABD đồng dạng tam giác ACE.
b) CM: HB.HD=HC.HE
c) Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc AMC=góc ANB=90 độ. CMR: AM=AN.




















