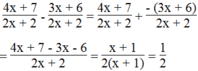62x + 14 = 50

Những câu hỏi liên quan
\(sin^62x+cos^62x=0\)
sin6(2x)+cos6(2x)=0
<=>(sin22x)3+(cos22s)3=0
<=> (sin22x+cos2x)[(sin42x-2sin22x.cos22x+cos42x)=0
<=>sin42x-2sin22x.cos22x+cos42x=0
đến đây bạn nhóm l;ại và giải
KQ là k có nghiệm
=> PT vô nghiệm
Đúng 0
Bình luận (1)
62x + 3.2x = 9.29
bài làm
62x+3.2x=9.29
62x+6x=261
62+6x=261
68x=261
x=261:68
x=\(\frac{261}{68}\)
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
x
2
-
6
2
x
+
18
≥
0
là A.
S
3
2
;
+
∞
B.
S
[
3
2
;
+
∞
)
C.
S
∅...
Đọc tiếp
Tập nghiệm của bất phương trình x 2 - 6 2 x + 18 ≥ 0 là
A. S = 3 2 ; + ∞
B. S = [ 3 2 ; + ∞ )
C. S = ∅
D. S = ℝ
Ta có: x 2 - 6 2 x + 18 = x - 3 2 2 ≥ 0 ∀ x
Tập nghiệm của bất phương trình x 2 - 6 2 x + 18 ≥ 0 là S= R.
Đúng 0
Bình luận (0)
Làm tính trừ phân thức: 4 x + 7 2 x + 2 - 3 x + 6 2 x + 2
giải hệ
x+y+2z=6
2x+y-z=1
-x+2y+z=3
Số tự nhiên �x thỏa mãn 3662�−1653662x−165 là
Đọc tiếp
Số tự nhiên thỏa mãn là
36 < 6\(2x-1\) < 65
62 < 6\(2x-1\) < 65
2 < 2\(x\) - 1 < 5
3 < 2\(x\) < 6
\(\dfrac{3}{2}\) < \(x\) < 6
\(1,5\) < \(x\) < 3
\(x\) = 2
Đúng 1
Bình luận (0)
Cho hệ phương trình
4
x
+
3
y
6
2
x
+
y
4
. Nghiệm của hệ phương trình là: A. (x; y) (−2; −3) B. (x; y) (−3...
Đọc tiếp
Cho hệ phương trình 4 x + 3 y = 6 2 x + y = 4 . Nghiệm của hệ phương trình là:
A. (x; y) = (−2; −3)
B. (x; y) = (−3; −2)
C. (x; y) = (−2; 3)
D. (x; y) = (3; −2)
Ta giải hệ phương trình bằng cách nhân hai vế của phương trình thứ hai với 2 rồi trừ từng vế của hai phương trình:
4 x + 3 y = 6 2 x + y = 4 ⇔ 4 x + 3 y = 6 4 x + 2 y = 8 ⇔ 4 x + 3 y = 6 y = − 2 ⇔ 4 x + 3 − 2 = 6 y = − 2 ⇔ x = 3 y = − 2
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (3; −2)
Đáp án: D
Đúng 0
Bình luận (0)
x^6+6x^5+17x^4+40x^3+62x^2+69x+76=0
63x(64-62)+62x(62-64)
5x(13-26)-26x(13-5)+21x13
63x(64-62)+62x(62-64)
=63x2+62x2
=(63+62)x2
=125x2
=250
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
4
x
+
3
y
6
2
x
+
y
4
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 4 x + 3 y = 6 2 x + y = 4
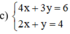 (Nhân cả hai vế của pt 2 với 2 để hệ số của x bằng nhau)
(Nhân cả hai vế của pt 2 với 2 để hệ số của x bằng nhau)
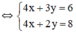 (Hệ số của x bằng nhau nên ta trừ từng vế của 2 pt)
(Hệ số của x bằng nhau nên ta trừ từng vế của 2 pt)
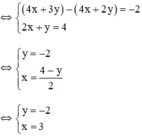
Vậy hệ phương trình có nghiệm duy nhất (3; -2).
Đúng 0
Bình luận (0)