cho tam giác ABC có AB =5 BC= 7 CA = 8. số đo góc A bằng ?
Tam giác ABC có AB =5; BC = 7; CA = 8. Số đo góc A ^ bằng:
A. 300
B. 450
C. 600
D. 900
Theo hệ quả định lí cosin, ta có cos A ^ = A B 2 + A C 2 − B C 2 2 A B . A C = 5 2 + 8 2 − 7 2 2.5.8 = 1 2 .
Do đó, A ^ = 60 ° .
Chọn C.
Tam giác ABC có AB = 5; BC = 7 và CA = 8. Số đo góc A bằng:
A. 450
B. 600
C. 1200
D. 300
Chọn B.
Theo định lí hàm cosin, ta có
![]()
Do đó ![]()
Cho tam giác ABC. Tính đường cao vẽ từ A và bán kính đường tròn ngoại tiếp tam giác biế
a. CA = 8 ; AB = 5 ; góc A bằng
b. BC = 21 ; CA = 17 ; AB = 8
a.
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=7\)
\(S=\dfrac{1}{2}AB.AC.sinA=10\sqrt{3}\)
\(\Rightarrow h_a=\dfrac{2S}{BC}=\dfrac{20\sqrt{3}}{7}\)
\(R=\dfrac{BC}{2sinA}=\dfrac{7\sqrt{3}}{3}\)
b.
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{11}{34}\)
\(\Rightarrow sinA=\dfrac{3\sqrt{115}}{34}\)
\(S=\dfrac{1}{2}AB.AC.sinA=6\sqrt{115}\)
\(h_a=\dfrac{2S}{BC}=\dfrac{4\sqrt{115}}{7}\)
\(R=\dfrac{BC}{2sinA}=...\)
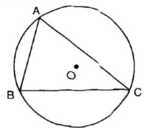
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75 0 , 2 x + 25 0 , 3 x - 22 ° . Một góc của tam giác ABC có số đo là:
( A ) 57 ° 5 ( B ) 59 ° ; ( C ) 61 ° ; ( D ) 60 °
Hãy chọn câu trả lời đúng.
Các cung 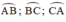 tạo thành một đường tròn
tạo thành một đường tròn
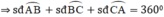
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
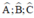 là các góc nội tiếp chắn các cung
là các góc nội tiếp chắn các cung 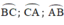
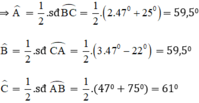
Vậy chọn đáp án C.
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75 0 , 2 x + 25 0 , 3 x − 22 0 . Một góc của tam giác ABC có số đo là:
( A ) 57 ° 5 ; ( B ) 59 ° ; ( C ) 61 ° ; ( D ) 60 °
Hãy chọn câu trả lời đúng.
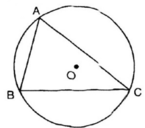
Các cung 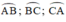 tạo thành một đường tròn
tạo thành một đường tròn
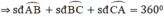
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
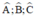 là các góc nội tiếp chắn các cung
là các góc nội tiếp chắn các cung 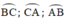
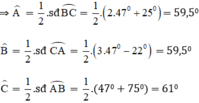
Vậy chọn đáp án C.
Bài 5: Cho tam giác ABC vuông cân tại A. Trên tia đối của tia BA lấy điểm D sao cho DB = BC. Tính số đo các góc của tam giác ACD
Bài6:TamgiácABCcântạiBcóBˆ =100 đôn.LấycácđiểmDvàEtrêncạnhAC sao cho AD = BA, CE = CB. Tính số đo góc DBE?
Bài 7: Cho tam giác ABC cân tại A. Vẽ BH vuông góc với AC tại H. Chứng minh rằng góc BAC có số đo gấp đôi số đo góc CBH.
Bài 8: Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD.
a) Chứng minh tam giác IBC và tam giác IDE là các tam giác cân.
b) Chứng minh BC // DE.
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng.
Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi
bài này dễ sao không biết
Bài 8 :
Tự vẽ hình nhé ?
a) Vì ∆ABC cân tại A (GT)
=> ∠ABC = ∠ACB (ĐN)
Mà ∠ABC + ∠DBC = 180o (2 góc kề bù)
∠ACB + ∠ECB = 180o (2 góc kề bù)
=> ∠DBC = ∠ECB (1)
Xét ∆BCD và ∆CBE có :
BD = CE (GT)
∠DBC = ∠ECB (Theo (1))
BC chung
=> ∆BCD = ∆CBE (c.g.c) (2)
=> ∠BCD = ∠CBE (2 góc tương ứng)
Hay ∠BCI = ∠CBI
Xét ∆IBC có : ∠BCI = ∠CBI (cmt)
=> ∆IBC cân tại I (định lý)
=> IB = IC (ĐN) (3)
Từ (2) => DC = EB (2 cạnh tương ứng)
Mà ID + IC = DC, IE + IB = EB
=> ID = IE
Xét ∆IDE có : ID = IE (cmt)
=> ∆IDE cân tại I (ĐN)
b) Ta có : AB + BD = AD
Mà AC + CE = AE
AB = AC (GT)
BD = CE (GT)
=> AD = AE
Xét ∆ADE có : AD = AE (cmt)
=> ∆ADE cân tại A (ĐN)
=> ∠ADE = \(\frac{180^o-\widehat{DAE}}{2}\)(4)
Vì ∆ABC cân tại A (GT)
=> ∠ABC = \(\frac{180^o-\widehat{BAC}}{2}\)(5)
Từ (4), (5) => ∠ADE = ∠ABC, mà 2 góc này ở vị trí đồng vị
=> BC // DE (DHNB)
c) Xét ∆ABM và ∆ACM có :
AM chung
AB = AC (GT)
MB = MC (do M là trung điểm của BC)
=> ∆ABM = ∆ACM (c.c.c)
=> ∠AMB = ∠AMC (2 góc tương ứng)
Mà ∠AMB + ∠AMC = 180o (2 góc kề bù)
=> ∠AMB = ∠AMC = 180o : 2 = 90o
Sau đó chứng minh ∆BIM = ∆CIM theo c.c.c bằng 3 yếu tố MI chung, MB = MC, IB = IC (Theo (3))
Rồi => ∠IMB = ∠IMC (tương ứng)
Mà ∠IMB + ∠IMC = 180o (kề bù)
=> ..... (làm như phần trên)
Ta có : ∠AMB + ∠IMB = ∠AMI
Mà ∠AMB = 90o (cmt)
∠IMB = 90o (cmt)
=> 90o + 90o = ∠AMI
=> ∠AMI = 180o
=> A, M, I thẳng hàng (đpcm)
Vậy .....
Có
\(AB^2=10^2\)
\(BC^2+AC^2=36+64=10^2\)
=> \(AB^2=AC^2+BC^2\)
=> t/g ABC vuông tại C
=> \(\widehat{ACB}=90^o\)
Bài 7: a, Cho tam giác ABC vuông tại A có AB 3 AC 4 = và BC = 5. Tính độ dài AB, AC b, Tính độ dài cạnh huyền biết độ dài hai cạnh góc vuông là 6 và 7 c, Tính góc ở đỉnh của tam giác cân biết số đo góc ở đáy là 200 d, Tính số đo góc ở đáy tam giác cân biết số đo góc ở đỉnh là 600
b: Độ dài cạnh huyền là \(\sqrt{6^2+7^2}=\sqrt{85}\left(cm\right)\)
c: Số đo góc ở đỉnh là:
\(180-2\cdot20^0=140^0\)
d: Số đó góc ở đáy là:
\(\dfrac{180^0-60^0}{2}=60^0\)
Cho tam giác ABC cân tại C có số đo góc A bằng 60 . Lấy các điểm D, E, F
theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF. Tam giác DEF là tam giác gì? Vì sao?
Lời giải:
Ta có : \(\Delta ABC\)là tam giác đều => \(\widehat{A}=\widehat{B}=\widehat{C}\)
Xét tam giác AFD và tam giác BED có :
AD = BE (gt)
\(\widehat{FAD}=\widehat{EBD}=60^0\)
AF = BD (gt)
=> \(\Delta AFD=\Delta BED\left(c-g-c\right)\)
=> DE = DF (hai cạnh tương ứng) (1)
Xét tam giác ADF và tam giác CEF có :
AD = CE (gt)
\(\widehat{DAF}=\widehat{ECF}=60^0\)
AF = CF (gt)
=> \(\Delta ADF=\Delta CEF\)(c-g-c)
=> DF = EF (hai cạnh tương ứng) (2)
Từ (1) và (2) => DE = DF = EF
Vậy \(\Delta DEF\)là tam giác đều