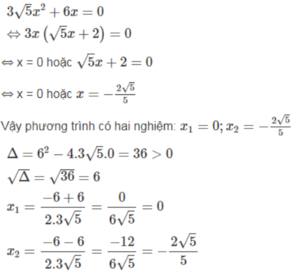Giải phương trình sau: x2 +6x + 5 =0

Những câu hỏi liên quan
Giải các phương trình sau bằng hai cách (phương trình tích; bằng công thức nghiệm) và so sánh kết quả tìm được: 3 5 x 2 + 6x = 0
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số. x 2 – 6x + 5 = 0
Ta có : x 2 – 6x + 5 = 0 ⇔ x 2 – 2.3x + 5 + 4 = 4
⇔ x 2 – 2.3x + 9 = 4 ⇔ x - 3 2 = 2 2
⇔ x – 3 = ± 2 ⇔ x – 3 = 2 hoặc x – 3 = -2
⇔ x = 1 hoặc x = 5
Vậy phương trình có hai nghiệm x 1 = 1, x 2 = 5
Đúng 0
Bình luận (0)
Giải các phương trình sau bằng cách biến đổi chúng thành những phương trình với vế trái là một bình phương còn vế phải là một hằng số. 3 x 2 – 6x + 5 = 0
Ta có : 3 x 2 – 6x + 5 = 0 ⇔ x 2 - 2x + 5/3 = 0
⇔ x 2 – 2x + 5/3 + 1 = 1 ⇔ x 2 – 2x + 1 = 1 - 5/3
⇔ x - 1 2 = -2/3
Ta thấy x - 1 2 ≥ 0 và -2/3 < 0
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
4
−
5
x
5
−
6
x
;
b)
3
x
+
2
−
7
x
+
1
0
;
c)...
Đọc tiếp
Giải các phương trình sau:
a) 4 − 5 x = 5 − 6 x ; b) 3 x + 2 − 7 x + 1 = 0 ;
c) x 2 − 2 x − 3 + x + 1 = 0 ; d) 1 4 x − 5 = 3 x + 1
a) Trường hợp 1. Xét 4 - 5x = 5 - 6x.
Tìm được x = 1.

Đúng 0
Bình luận (0)
Giải các phương trình sau:
a
)
(
x
–
1
)
(
x
2
+
x
+
1
)
–
2
x
x
(
x
–
1
)
(
x
+
1
)
b
)
x
2
–
...
Đọc tiếp
Giải các phương trình sau:
a ) ( x – 1 ) ( x 2 + x + 1 ) – 2 x = x ( x – 1 ) ( x + 1 ) b ) x 2 – 3 x – 4 = 0
c ) 1 x - 5 - 3 x 2 - 6 x + 5 = 5 x - 1
d ) 2 x - 1 - 3 x 2 x 3 - 1 = x x 2 + x + 1
a) (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1)
⇔ x2 – 1 – 2x = x3 – x
⇔ -2x + x = 1 ⇔ - x = 1 ⇔ x = -1
Tập nghiệm của phương trình: S = { -1}
b) x2 – 3x – 4 = 0
⇔ x2 – 4x + x – 4 = 0 ⇔ x(x – 4) + (x – 4) = 0
⇔ (x – 4)(x + 1) = 0 ⇔ x – 4 = 0 hoặc x + 1 = 0
⇔ x = 4 hoặc x = -1
Tập nghiệm của phương trình: S = {4; -1}
c) ĐKXĐ : x – 1 ≠ 0 và x2 + x + 1 ≠ 0 (khi đó : x3 – 1 = (x – 1)(x2 + x + 1) ≠ 0)
⇔ x ≠ 1
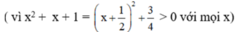
Quy đồng mẫu thức hai vế:
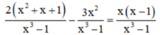
Khử mẫu, ta được: 2x2 + 2x + 2 – 3x2 = x2 – x
⇔ -2x2 + 3x + 2 = 0 ⇔ 2x2 – 3x – 2 = 0
⇔ 2x2 – 4x + x – 2 = 0 ⇔ 2x(x – 2) + (x – 2) = 0
⇔ (x – 2)(2x + 1) = 0 ⇔ x – 2 = 0 hoặc 2x + 1 = 0
⇔ x = 2 hoặc x = -1/2(thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {2 ; -1/2}
d) ĐKXĐ : x – 5 ≠ 0 và x – 1 ≠ 0 (khi đó : x2 – 6x + 5 = (x – 5)(x – 1) ≠ 0)
Quy đồng mẫu thức hai vế :
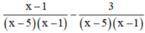
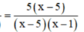
Khử mẫu, ta được : x – 1 – 3 = 5x – 25 ⇔ -4x = -21
⇔ x = 21/4 (thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {21/4}
Đúng 0
Bình luận (0)
Xác định a, b’,c trong mỗi phương trình rồi giải phương trình bằng công thức nghiệm thu gọn: 5 x 2 – 6x -1 = 0
Phương trình 5 x 2 – 6x -1 = 0 có hệ số a = 5, b’ = -3, c = -1
Ta có: ∆ ’ = b ' 2 – ac = - 3 2 -5.(-1) = 9 + 5 = 14 > 0
∆ ' = 14
Phương trình có hai nghiệm phân biệt :
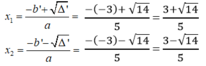
Đúng 0
Bình luận (0)
BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn). 1) x2 - 11x + 38 = 0 ; 2) 6x2 + 71x + 175 = 0 ; 3) 5x2 - 6x + 27 = 0 ; 4) - 30x2 + 30x - 7,5 = 0 ; 5) 4x2 - 16x + 17 = 0 ; 6) x2 + 4x - 12 = 0 ;
1, \(\Delta=\left(-11\right)^2-4.1.38=121-152=-31< 0\)
\(\Rightarrow\) pt vô nghiệm
2, \(\Delta=71^2-4.6.175=5041-4200=841\)
\(x_1=\dfrac{-71+\sqrt{841}}{2.6}=\dfrac{-71+29}{12}=\dfrac{-42}{12}=-\dfrac{7}{2}\)
\(x_2=\dfrac{-71-\sqrt{841}}{2.6}=\dfrac{-71-29}{12}=\dfrac{-10}{12}=-\dfrac{25}{3}\)
3, \(\Delta=\left(-3\right)^2-5.27=9-135=-126< 0\)
⇒ pt vô nghiệm
4, \(\Delta=15^2-\left(-30\right)\left(-7,5\right)=225-225=0\)
\(\Rightarrow x_1=x_2=\dfrac{-30}{2.\left(-30\right)}=\dfrac{1}{2}\)
5, \(\Delta'=\left(-8\right)^2-4.17=64-68=-4\)
⇒ pt vô nghiệm
6, \(\Delta=4^2-4.1.\left(-12\right)=16+48=64\)
\(x_1=\dfrac{-4+\sqrt{64}}{2.1}=\dfrac{-4+8}{2}=\dfrac{4}{2}=2\)
\(x_2=\dfrac{-4-\sqrt{64}}{2.1}=\dfrac{-4-8}{2}=\dfrac{-12}{2}=-6\)
Đúng 1
Bình luận (1)
Giải các phương trình sau:a)
x
+
3
3
−
x
−
1
3
0
;
b)
x
4
+
x
2
−
2
0
;
c)
x
3...
Đọc tiếp
Giải các phương trình sau:
a) x + 3 3 − x − 1 3 = 0 ;
b) x 4 + x 2 − 2 = 0 ;
c) x 3 + 3 x 2 + 6 x + 4 = 0 ;
d) x 3 − 6 x 2 + 8 x = 0 .
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được ![]()
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
Đúng 0
Bình luận (0)
giải các bất phương trình sau
a, <x-3>*<x2+x-20>≥0
b, x2-4x-5 /2x+4 ≥0
c, -1/x2-6x+8≤1
a, \(\left(x-3\right)\left(x^2+x-20\right)\ge0\)
\(\Leftrightarrow\) \(\left(x-3\right)\left(x-4\right)\left(x+5\right)\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x+5=0\Leftrightarrow x=-5\)
+) Lập trục xét dấu f(x) (Bạn tự kẻ trục nha)
\(\Rightarrow\) Bpt có tập nghiệm S = \(\left[-5;3\right]\cup\) [4; \(+\infty\))
b, \(\dfrac{x^2-4x-5}{2x+4}\ge0\)
\(\Leftrightarrow\) \(\dfrac{\left(x-5\right)\left(x+1\right)}{2x+4}\ge0\)
+) \(x-5=0\Leftrightarrow x=5\); \(x+1=0\Leftrightarrow x=-1\); \(2x+4=0\Leftrightarrow x=-2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (-2; -1] \(\cup\) [5; \(+\infty\))
c, \(\dfrac{-1}{x^2-6x+8}\le1\)
\(\Leftrightarrow\) \(\dfrac{\left(x-3\right)^2}{\left(x-4\right)\left(x-2\right)}\ge0\)
+) \(x-3=0\Leftrightarrow x=3\); \(x-4=0\Leftrightarrow x=4\); \(x-2=0\Leftrightarrow x=2\)
+) Lập trục xét dấu f(x)
\(\Rightarrow\) Bpt có tập nghiệm S = (\(-\infty\); 2) \(\cup\) (4; \(+\infty\))
Chúc bn học tốt!
Đúng 2
Bình luận (0)
Giải các phương trình : - 2 x 2 +6x = 0
Ta có: - 2 x 2 + 6x = 0 ⇔ x(6 - 2 x) = 0
⇔ x = 0 hoặc 6 - 2 x = 0 ⇔ x = 0 hoặc x = 3 2
Vậy phương trình có hai nghiệm x 1 = 0, x 2 = 3 2
Đúng 0
Bình luận (0)