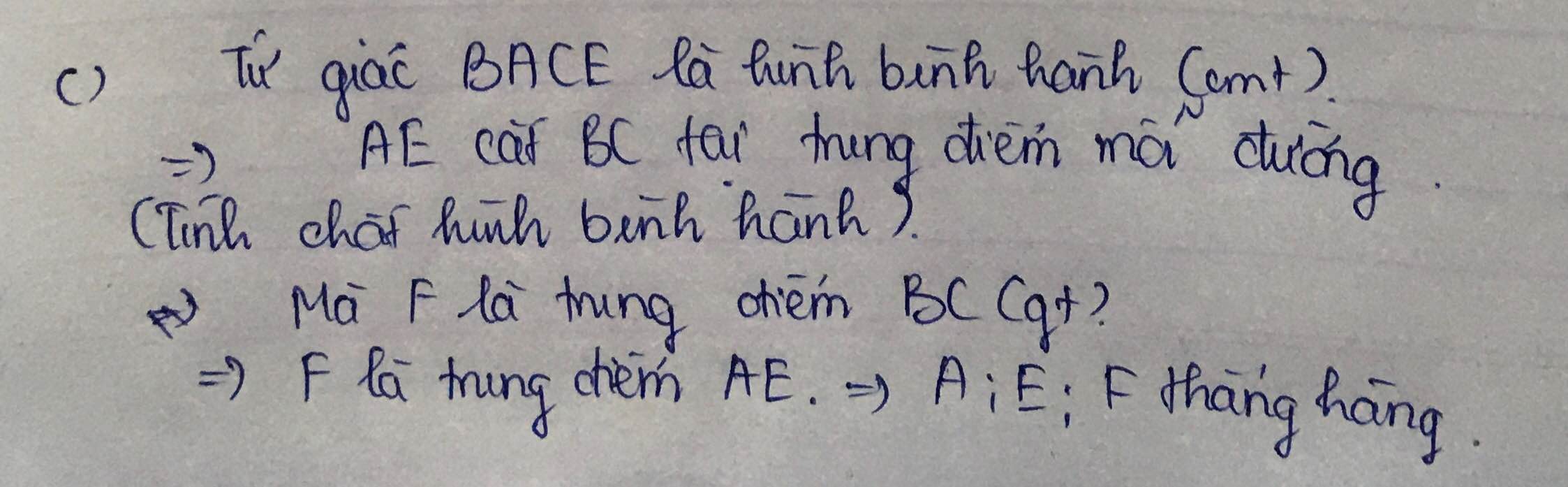cho tam giác ABC, gọi M là trung điểm của AB. Chứng minh rằng, MC nhỏ hơn AC+ BC/2

Những câu hỏi liên quan
1 ) Cho tam giác ABC . Gọi M là một điểm nằm trong tam giác . Chứng minh rằng : MA + MB + MC > nửa chu vi tam giác đó
2 ) Cho tam giác ABC . Gọi M là trung điểm cạnh BC . Chứng minh rằng : AM < AB + AC / 2
Cho tam giác ABC có AB =AC và M là trung điểm của BC .Gọi N là trung điểm của AB,tìm tia đối của tia MC lấy điểm K sao cho NK=NC a.Chứng minh tạm giác ABM=Tam giác ACM b.chứng minh rằng AK =2×MC
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét tứ giác AKBC có
N là trung điểm của AB
N là trung điểm của KC
Do đó: AKBC là hình bình hành
Suy ra: AK=BC
hay AK=2xMC
Đúng 0
Bình luận (0)
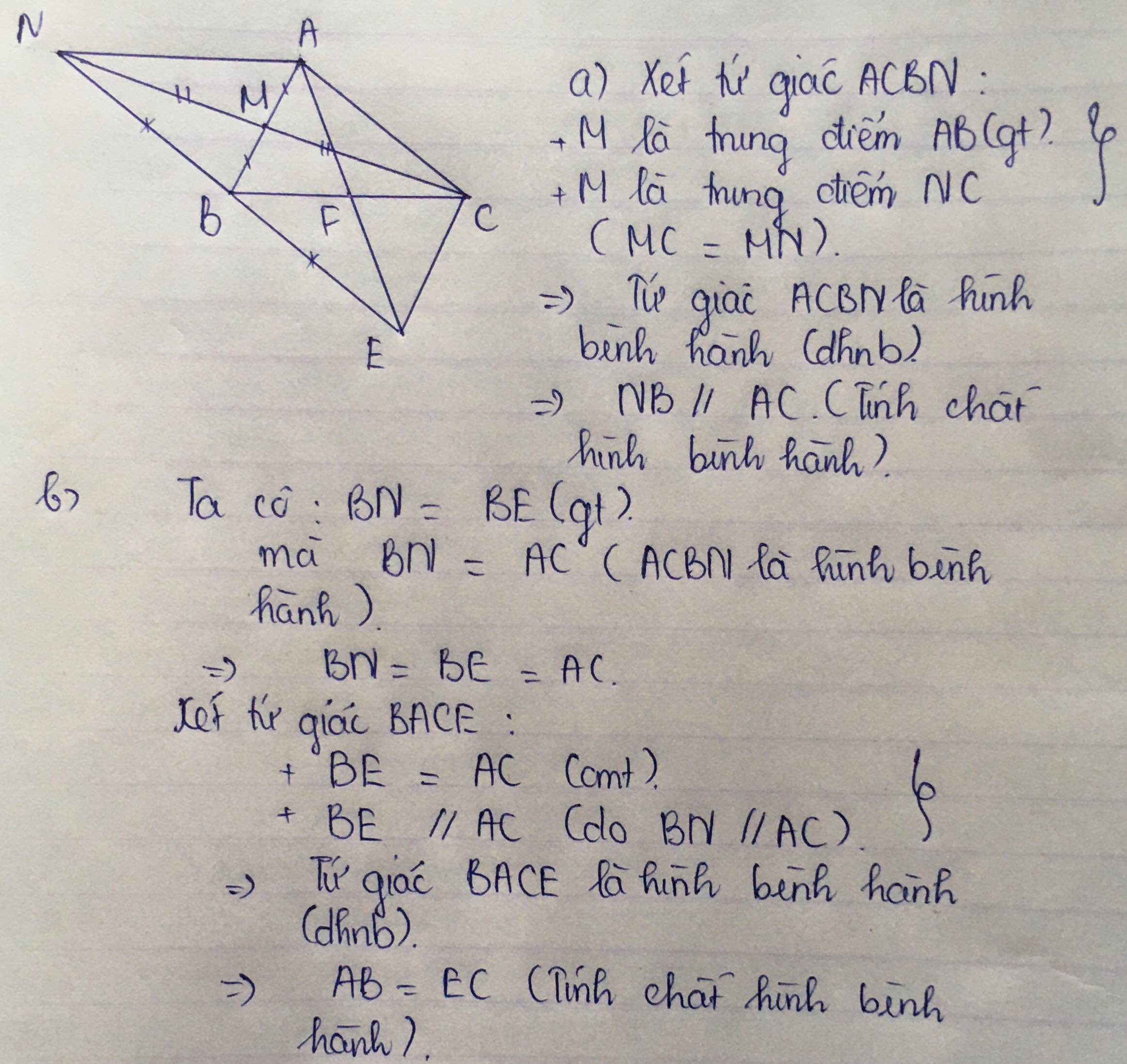
cho tam giác ABC,M là trung điểm của AB. Trên tia đối của tia MC lấy điểm N sao cho MC =MN
A. chứng minh rằng NB//AC
B. trên tia đối tia BN lấy điểm E sao cho BN=BE. Chứng minh: AB=EC
C. gọi F là trung điểm của BC. Chứng minh A,E,F thẳng hàng
tham khảo
mik ko thể vẽ hình đc
SORRY
Giải thích các bước giải:
a.*Xét ΔMBN,ΔMAC có:
MA=MB( vì M là trung điểm BA)
ˆNMB=ˆMC (2 góc đối đỉnh)
MN=MC
⇔ΔMNB=ΔMCA(c.g.c)
⇒ˆMNB=ˆMCA
⇒BN//AC
Vậy BN//AC
b.Từ câu a ⇒AC=BN
Ta có
BN//AC
⇒AC//BE
⇒ˆEAC=ˆAEB
*Xét ΔABE,ΔECA có:
AE chung
ˆAEB=ˆEAC
BE=AC
⇔ ΔABE=ΔECA(c.g.c)
⇒AB=EC
Vậy AB=EC
c.Ta có
AC//BE
⇒ˆACB=ˆCBE
⇒ˆACF=ˆFBE
*Xét ΔACF và ΔBEF có:
FB=FC( F là trung điểm của BC)
ˆACF=ˆEBF
AC=BE
⇔ΔACF=ΔEBF(c.g.c)
⇒ˆAFC=ˆBFE
⇒A,F,E thẳng hàng
Vậy A;F;E thẳng hàng
Đúng 0
Bình luận (1)
4) cho tam giác ABC có AB=AC mà M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của tia NC lấy điểm K sao cho NK=NC
a)chứng minh tam giác ABM= tam giác ACM
b)chúng minh rằng AK= 2.MC
c)tính số đo của MAK ?
5)cho 2a=3b=4c. tìm giá trị của biểu thức A=\(\dfrac{a-b+c}{a+2b-c}\)
Bài 4:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Xét tứ giác AKBC có
N là trung điểm của AB
N là trung điểm của CK
Do đó: AKBC là hình bình hành
Suy ra: AK=BC
hay AK=2MC
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥BC
mà BC//AK
nên AM⊥AK
hay \(\widehat{MAK}=90^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=AC, M là trung điểm của AB.M là trung điểm AB,AE là tia phân giác góc BAC (E thuộc BC).Trên tia đối của tia MC lấy điểm K sao cho MC=MK
a. Chứng minh rằng: BK//AC
b. Chứng minh tam giác ACE=tam giác ABE
c. Trên tia AB lấy điểm D( B nằm giữa A và D), trên tia AC lấy điểm E( C nằm giữa A và E) sao cho BD= CE. Chứng minh rằng BE= CD.
a: Xét tứ giác AKBC có
M là trung điểm của đường chéo CK
M là trung điểm của đường chéo AB
Do đó: AKBC là hình bình hành
Suy ra: BK//AC
b: Xét ΔABE và ΔACE có
AB=AC
\(\widehat{BAE}=\widehat{CAEE}\)
AE chung
Do đó: ΔABE=ΔACE
Đúng 0
Bình luận (0)
Cho tam giác abc có ba góc nhọn biết AB nhỏ hơn AC Gọi M N lần lượt là trung điểm của AB AC a)Chứng minh tứ giác mncb là hình thang b) Gọi D là trung điểm của BC Chứng minh tứ giác MNCD là hình bình hành c) Gọi E là điểm đối xứng của d qua n Chứng minh tứ giác ADCE là hình bình hành d) tam giác ABC cần thêm điều kiện gì để tam giác tứ giác ABCE thành hình chữ nhật
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
hay MNCB là hình thang
b: Xét tứ giác MNCD có
MN//CD
MN=CD
Do đó: MNCD là hình bình hành
c: Xét tứ giác ADCE có
N là trung điểm của AC
N là trung điểm của DE
Do đó:ADCE là hình bình hành
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB < AC), có ba góc nhọn nội tiếp đường tròn (O). M là một điểm trên cung nhỏ AC sao cho MA < MC. Vẽ MH vuông góc với BC tại H. MT vuông góc với AC tại M.
a) Chứng minh rằng: góc IHM = góc HMI
b) Chúng minh rằng: tam giác BMA đồng dạng với tam giác HMI
c) Gọi E là trung điểm của HI, F là trung điểm của AB, chứng minh ME vuông góc với EF
Cho tam giác ABC, gọi M là trung điểm của BC. Chứng minh rằng \(\dfrac{AB+AC-BC}{2}\) < AM < \(\dfrac{AB+AC}{2}\)
Cho tam giác ABC có AB=AC, M là trung điểm của AB.M là trung điểm AB,AE là tia phân giác góc BAC (E thuộc BC).Trên tia đối của tia MC lấy điểm K sao cho MC=MK
a. Chứng minh rằng: BK//AC
b. Chứng minh tam giác ACE=tam giác ABE
c. đường thẳng KB cắt AE ở I.CM tam giác IAK vuông
a: Xét tứ giác AKBC có
M là trung điểm của đường chéo CK
M là trung điểm của đường chéo AB
Do đó: AKBC là hình bình hành
Suy ra: BK//AC
b: Xét ΔABE và ΔACE có
AB=AC
\(\widehat{BAE}=\widehat{CAEE}\)
AE chung
Do đó: ΔABE=ΔACE
Đúng 0
Bình luận (0)