cho hình như sau
o o o o o o o o o o} 10
vậy 4/5 của 10 là
Cho 4 hình tròn tâm O1, O2, O3, O4, O5, như trên hình vẽ. Các hình tròn O1, O2, O3, O4 cùng tiếp xúc với O5. Hình tròn O1 tiếp xúc với hình tròn O2, hình tròn O2 tiếp xúc với hình tròn O3, hình tròn O3 tiếp xúc với hình tròn O4, hình tròn O4 tiếp xúc với hình tròn O1. Các hình tròn O1, O2, O3, O4 lần lượt có độ dài bán kính là 50, 200, 80, 90. Tính độ dài bán kính của hình tròn O5.
1 o to di tu A den B trong 5 gio trong 2 gio dau o to dai voi van toc 40 km/gio3 gio sauo to di duoc voi van toc 50 km/giotinh van toc rtrung binh o to di tu A den B
CHo tứ giác ABCD .vẽ ra phía ngoài tứ giác đó các hình vuông ABEF, BCGH,CDPQ,ADRS. Gọi O1,O2,O3,O4lần lượt là tâm của hình vuông trên. CMR: O1O3=O2O4 , O1O3\(\perp O_2O_4\)
Cho hai đường tròn (O; 4 cm), (O'; 5 cm) và OO’= 6cm. Vị trí tương đối của (O) và (O’) là:
4 o/o của 2500 kg là: ...........
10 o/o của 1200 lít là: .........
25 o/o của 4000 m2 là:..........
4% của 2500 kg = 100 kg
10% của 1200 l = 120 l
25% của 4000m2 = 1000m2
Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O;R),(O′;R). Biết rằng tồn tại dây cung AB của đường tròn O sao cho O′AB là tam giác đều và (O′AB) hợp với đường tròn O một góc 60 o . Tính diện tích xung quanh của hình trụ.
A. π 7 R 2 7
B. 4 π 7 R 2 7
C. 2 π 7 R 2 7
D. 6 π 7 R 2 7
Cho hình vuông ABCD, hình tròn tâm O (như hình vẽ).
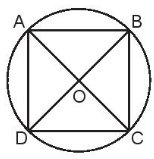
a) Nêu tên ba điểm thẳng hàng.
b) O là trung điểm của những đoạn thẳng nào?
c) Dùng ê ke kiểm tra rồi nêu tên các góc vuông đỉnh O.
a) Ba điểm thẳng hàng là: A, O, C và D, O, B.
b) O là trung điểm của đoạn thẳng AC và BD.
c) Các góc vuông đỉnh O là:
Góc vuông đỉnh O cạnh OA, OB.
Góc vuông đỉnh O cạnh OB, OC.
Góc vuông đỉnh O cạnh OC, OD.
Góc vuông đỉnh O cạnh OD, OA.
Bài 10: Cho đường tròn (O) cắt (O') tại A, B (O, O' nằm khác phía so với AB). Kẻ đường kính AC của (O) và đường kính AD của (O').
a) Chứng minh B, C, D thẳng hàng.
b) Gọi giao điểm thứ 2 của CA với (O') là E, của DA với (O) là F. Chứng minh: C, D, E, F cùng thuộc một đường tròn.
c) Chứng minh: A là tâm đường tròn nội tiếp tam giác BEF.
d) Chứng minh: CF, BA, DE đồng quy.
Số phát biểuđúng là:
1.Phép đối xứng qua điểm O là một phép dời hình.
2. Phép đối xứng qua điểm O là phép quay tâm O góc quay 180 °
3. Phép quay Q(O; α ) biến A thành M thì O cách đều A và M
4. Phép quay Q(O; α ) biến A thành M thì O thuộc đường tròn đường kính AM
5. Phép quay Q(O; α ) biến O thành chính nó
6.Phép quay Q(O; α ) biến (O;R) thành (O;2R)
7.Phép quay tâm O góc π 2 và phép quay tâm O góc 5 π 2 là hai phép quay giống nhau
A.4
B.5
C.6
D.7
Đáp án B
Những phát biểuđúng: 1;2;3;5;7
4. Phép quay Q(O;180 ° ) biến A thành M thì O thuộc đường tròn đường kính AM
6. Phép quay Q(O; α ) biến (O;R) thành (O;R)