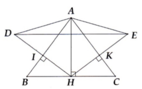
Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh rằng H là

trung điểm của đoaṇ thẳng BC

b) Tính độ dài đoạn thẳng AH
c) Kẻ HI AB taị I và HK  AC taị K. Vẽ các điểm D và E sao cho I ,K lần lươṭ là

trung điểm

của HD và HE. Chứng minh AE = AH . Tam giác ADE là tam giác gì? Vì sao?
d) Chứng minh AH là đường trung trực của đoạn thẳng DE .
e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE

Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh rằng H là

trung điểm của đoaṇ thẳng BC

b) Tính độ dài đoạn thẳng AH
c) Kẻ HI AB taị I và HK  AC taị K. Vẽ các điểm D và E sao cho I ,K lần lươṭ là

trung điểm

của HD và HE. Chứng minh AE = AH . Tam giác ADE là tam giác gì? Vì sao?
d) Chứng minh AH là đường trung trực của đoạn thẳng DE .
e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE

Cho tam giác ABC có AB=AC = 10cm, BC = 12cm. Kẻ A H ⊥ B C  tại H.

a) Chứng minh rằng ∆ A B H   = ∆ A C H . Từ đó suy ra H là trung điểm của đoạn thẳng BC.

b) Tính độ dài đoạn thẳng AH.

c) Kẻ H I ⊥ A B tại I và H K ⊥ A C  tại K. Vẽ các điểm D và E sao cho I, K lần lượt là trung điểm của HD và HE. Chứng minh: AE = AH

d) Tam giác ADE là tam giác gì? Vì sao? Chứng minh DE // BC.

e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE.

Cho tam giác ABC có AB = AC =10 cm ; BC =12cm . Kẻ AH vuông góc BC  tại H .

 a) Chứng minh tam giác ABH = tam giác ACH . Từ đó suy ra H là trung điểm của đoạn thẳng BC .

 b) Tính độ dài đoạn thẳng AH .

 c) Kẻ HI vuông góc AB tại I ; HK vuông góc  AC tại K . Vẽ các điểm D E, sao cho I, K lần lượt là trung điểm của HD HE , . Chứng minh AE = AH  .

 d) tam giác ADE là tam giác gì? Vì sao? Chứng minh DE / / BC . 

 e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE . 

Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh rằng H là

trung điểm của đoaṇ thẳng BC

b) Tính độ dài đoạn thẳng AH
c) Kẻ HI AB taị I và HK  AC taị K. Vẽ các điểm D và E sao cho I ,K lần lươṭ là

trung điểm

của HD và HE. Chứng minh AE = AH . Tam giác ADE là tam giác gì? Vì sao?
d) Chứng minh AH là đường trung trực của đoạn thẳng DE .
e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE

Cho tam giác ABC có AB = AC = 10cm, BC = 12cm. Kẻ AH vuông góc với BC tại H
a) Chứng minh rằng H là

trung điểm của đoaṇ thẳng BC

b) Tính độ dài đoạn thẳng AH
c) Kẻ HI AB taị I và HK  AC taị K. Vẽ các điểm D và E sao cho I ,K lần lươṭ là

trung điểm

của HD và HE. Chứng minh AE = AH . Tam giác ADE là tam giác gì? Vì sao?
d) Chứng minh AH là đường trung trực của đoạn thẳng DE .
e) Tìm điều kiện của tam giác ABC để A là trung điểm của DE

Cho tam giác ABC có AB= AC =10cm, BC=12cm,kẻ AH vuông góc vs BC tại H 1. Chứng minh tam giác ABH=ACH và H là trung điểm của BC 2. Tính AH? 3. Kẻ IH vuông góc vs AB tại I, kẻ HK vuông góc vs AC tại K. Vẽ các điểm D và E sao cho I và K lần lượt là trung điểm của HD và HE. Chứng minh AE=AH 4. Tam giác ADE là tam giác gì? Vì sao? 5. Chứng minh DE song song vs BC 6. Tam giác ABC cần thỏa mãn điều kiện gì để A là trung điểm của DE Giải giúp mình với cám ơn!!!

Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H.
1) Chứng minh tam giác ABH = tam giác ACH và H là trung điểm của BC.
2) Nếu có AB = 10cm, BC = 12 cm, hãy tính độ dài đoạn thẳng AH.
3) Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Lấy các điểm M và N sao cho E là trung điểm của HM, F là trung điểm của HN. Chứng minh AN = AH.
4) Tam giác ABC cần thêm điều kiện gì thì A là trung điểm của MN?
Giúp mik vs ạ mik đang cần gấp.

Bài 1:Cho tam giác ABC có AB=AC=10cm,BC=12cm,kẻ AH vuông góc với BC tại H

a,Chứng minh tam giác ABH=tam giác ACH

b,Tính độ dài AH

c,Kẻ HI vuông góc với AB tại I,HK vuông góc với AC tại K vẽ các điểm D và E sao cho I,K lần lượt là trung điểm của HD,HE.Chứng minh AE=AH=AD

d,Tam giác ADE là tam giác gì?vì sao?Chứng minh DE song song BC

e,Tìm điều kiện của tam giác ABC để A là trung điểm của DE

 CÁC BẠN GIÚP MK VS