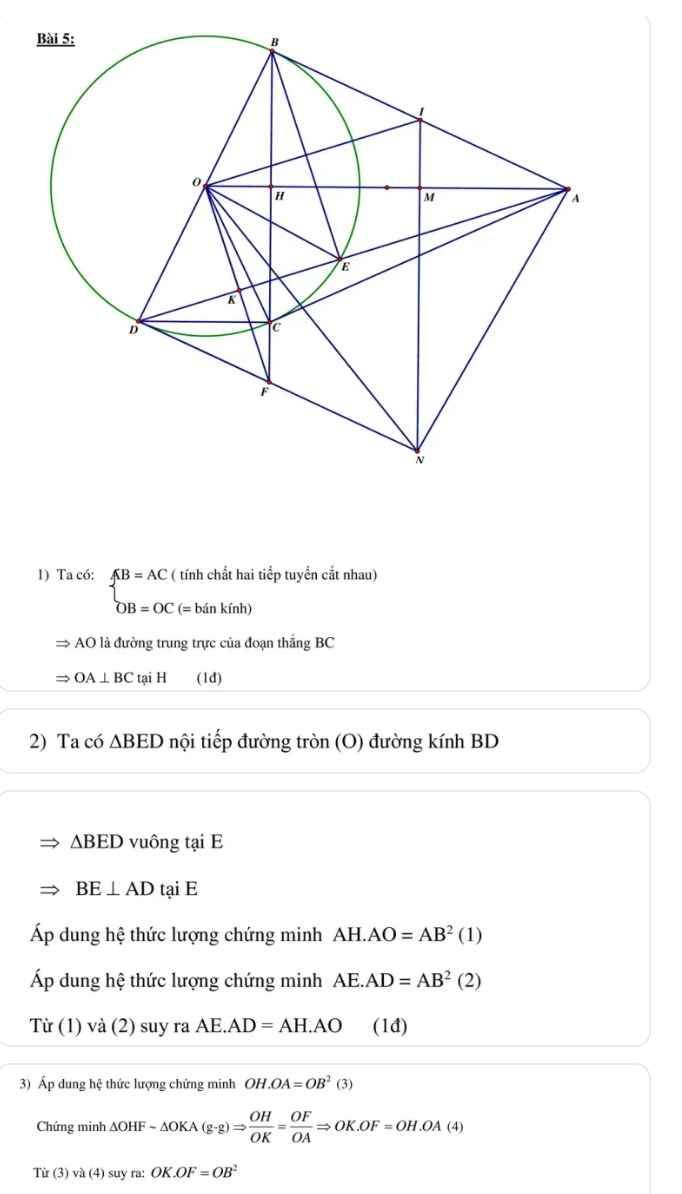
Từ điểm A nằm ngoài đường tròn (O;R) vẽ một đường thẳng d vuông góc với OA tại A . Gọi M là một điểm tùy ý trên d . Vẽ tiếp tuyến MB và MC với (O;R) ( B,C là hai tiếp điểm ) . OM cắt BC tại H
a) chứng minh ; 5 điểm O,B,M,A,C cùng nằm trên 1 đường tròn
b) Gọi D là một điểm trên cung nhỏ BC của đường tròn (O) (cung DB < cung DC ). Đường thẳng DH cắt đường tròn (O) tại điểm thứ 2 là K . Chứng tỏ ; MO là phân giác của góc DMK
c) chứng tỏ ; Khi M di động trên d thì BC luôn đi qua một điểm cố định và H di động trên một đường cố định
d) Cho biêt1 OA= 3R . TÌm vị trí điểm M trên d sao cho tứ giác OBMC có diện tích nhỏ nhất.
( siêu khó :)) . Giải dùm )