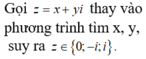Tìm nghiệm của phương trình sau: ( x - z )( x2 + xz + z2 ) = xy3 + 3z3

Những câu hỏi liên quan
Biết phương trình
a
z
3
+
b
z
2
+
c
z
+
d
0
(
a
,
b
,
c
,
d
∈
R
)
có z1, z2, z3 là các nghiệm, biết rằng
z
3
1
+
2
i
là nghiệm của phương trình. Biết z2 có...
Đọc tiếp
Biết phương trình a z 3 + b z 2 + c z + d = 0 ( a , b , c , d ∈ R ) có z1, z2, z3 là các nghiệm, biết rằng z 3 = 1 + 2 i là nghiệm của phương trình. Biết z2 có phần ảo âm. Tìm phần ảo của số phức w = z 1 + 2 z 2 + 3 z 3
A. 3
B. 2
C. -2
D. -1
Biết phương trình
a
z
3
+
b
z
2
+
c
z
+
d
0
(
a
,
b
,
c
,
d
∈
R
)
có z1, z2, z3 là các nghiệm, biết rằng z31+2i là nghiệm của phương trình. Biết z2 có phần ảo âm. Tìm phần ảo của số phức
w
z...
Đọc tiếp
Biết phương trình a z 3 + b z 2 + c z + d = 0 ( a , b , c , d ∈ R ) có z1, z2, z3 là các nghiệm, biết rằng z3=1+2i là nghiệm của phương trình. Biết z2 có phần ảo âm. Tìm phần ảo của số phức w = z 1 + 2 z 2 + 3 z 3
![]()
![]()
![]()
![]()
Biết phương trình
z
4
-
3
z
3
+
4
z
2
-
3
z
+
1
0
có 3 nghiệm phức
z...
Đọc tiếp
Biết phương trình z 4 - 3 z 3 + 4 z 2 - 3 z + 1 = 0 có 3 nghiệm phức z 1 , z 2 , z 3 . Tính giá trị của biểu thức T = z 1 + z 2 + z 3
A. T = 3
B. T = 4
C. T = 1
D. T = 2
Chọn đáp án A
*Với z=0 thì phương trình đã cho trở thành 1=0 (Vô lý).
*Với z ≠ 0 ta chia cả hai vế của phương trình cho z 2 và được
![]()
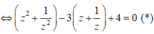
![]()
![]()
Phương trình (*) trở thành
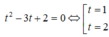
![]()
![]()
![]()
![]()
Vậy T = z 1 + z 2 + z 3 = 3
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của tham số m (biết
m
≥
-
2019
) để hệ phương trình sau có nghiệm thực?
x
2
+
x
-
y
3
1
-
2...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m (biết m ≥ - 2019 ) để hệ phương trình sau có nghiệm thực?
x 2 + x - y 3 = 1 - 2 m 2 x 3 - x 2 y 3 - 2 x 2 + x y 3 = m
A. 2021
B. 2019
C. 2020
D. 2018
cho x+y+z=4 xy+xz+xt+yz+yt+zt=1 tìm GTNN của x2+y2+z2+t2
bài 1 phân tích các đa thức thành nhân tử a) x2 - z2 + y2 - 2xy b) a3 - ay - a2x + xy c) x2 - 2xy + y2 - xz + yz d) x2 - 2xy + tx - 2ty bài 2 giải các phương trình sau ( x - 2 )2 - ( x - 3 ) ( x+ 3 ) 6 bài 3 chứng minh rằng a) x2 + 2x + 2 0 với xϵZb) -x2 + 4x - 5 0 với x ϵ Z
Đọc tiếp
bài 1 phân tích các đa thức thành nhân tử
a) x2 - z2 + y2 - 2xy b) a3 - ay - a2x + xy
c) x2 - 2xy + y2 - xz + yz d) x2 - 2xy + tx - 2ty
bài 2 giải các phương trình sau
( x - 2 )2 - ( x - 3 ) ( x+ 3 ) = 6
bài 3 chứng minh rằng
a) x2 + 2x + 2 > 0 với xϵZ
b) -x2 + 4x - 5 < 0 với x ϵ Z
\(1,\\ a,=\left(x-y\right)^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\\ b,=a^2\left(a-x\right)-y\left(a-x\right)=\left(a^2-y\right)\left(a-x\right)\\ c,=\left(x-y\right)^2-z\left(x-y\right)=\left(x-y\right)\left(x-y-z\right)\\ d,=x\left(x-2y\right)+t\left(x-2y\right)=\left(x+t\right)\left(x-2y\right)\\ 2,\\ \Rightarrow x^2-4x+4-x^2+9=6\\ \Rightarrow-4x=-7\Rightarrow x=\dfrac{7}{4}\\ 3,\\ a,x^2+2x+2=\left(x+1\right)^2+1\ge1>0\\ b,-x^2+4x-5=-\left(x-2\right)^2-1\le-1< 0\)
Đúng 1
Bình luận (1)
Tìm tập nghiệm phức của phương trình
z
2
+
|
z
|
0
Đọc tiếp
Tìm tập nghiệm phức của phương trình z 2 + | z | = 0
![]()
![]()
![]()
![]()
Tìm tập nghiệm phức của phương trình
z
2
+
z
0
. A.
0
;
-
1
;
-
i
B.
0
;
-
1
;
i
C.
0...
Đọc tiếp
Tìm tập nghiệm phức của phương trình z 2 + z = 0 .
A. 0 ; - 1 ; - i
B. 0 ; - 1 ; i
C. 0 ; 1 ; - i
D. 0 ; i ; - i
Chọn D
Gọi z=x+yi thay vào phương trình tìm x, y, suy ra zÎ{0;-i;i}
Đúng 0
Bình luận (0)
Tìm các nghiệm số nguyên của phương trình sau đây \(\left(x-z\right)\left(x^2+xz+z^2\right)=xy^3+3z^3\)