Cho tam giác ABC vuông tại A, điểm H nằm giữa A và C. So sánh BH và BC.

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, điểm H nằm giữa A và C. So sánh BH và BC. E cần gấp ạ
Câu 1: Cho △ABC có góc B 50 độ.a, So sánh các cạnh của △ABCb, Kẻ AH vuông góc với BC tại H. So sánh độ dài cạnh HB và HC Câu 2: Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Kẻ BH và CK vuông góc với đường thẳng AD tại H và Ka, So sánh BH + CK và AB + ACb, So sánh BH + CK và BCNếu△ABC vuông tại B và D là trung điểm BC thì so sánh AH + Ak với 2. AB
Đọc tiếp
Câu 1: Cho △ABC có góc B = 50 độ.
a, So sánh các cạnh của △ABC
b, Kẻ AH vuông góc với BC tại H. So sánh độ dài cạnh HB và HC
Câu 2: Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Kẻ BH và CK vuông góc với đường thẳng AD tại H và K
a, So sánh BH + CK và AB + AC
b, So sánh BH + CK và BC
Nếu△ABC vuông tại B và D là trung điểm BC thì so sánh AH + Ak với 2. AB
a: BH<AB
CK<AC
=>BH+CK<AB+AC
b: BH<BD
CK<CD
=>BH+CD<BD+CD=BC
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Gọi H và K là chân đường vuông góc kẻ từ B và C đến đường thẳng AD:
a) So sánh BH+CK và AB+AC.
b) So sánh BH+CK và BC
cho tam giác abc có góc a tù ab<ac kẻ ah vg góc vs bc tại h
a so sánh bh và ch
b gọi m là 1 điểm nằm giữa a và h so sánh mb vàmc
a: Xét ΔABC có AB<AC
mà HB,HC lần lượt là hình chiếu của AB,AC
nên HB<HC
b: Xét ΔMBC có
HB,HC lần lượt là hình chiếu của MB,MC trên BC
HB<HC
=>MB<MC
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Gọi H và K là chân đường vuông góc kẻ từ B và C đến đường thẳng AD:
a) So sánh BH+CK và AB+AC.
b) So sánh BH+CK và BC
Bài 1:Cho tam giác ABC vuông góc tại A,tia phân giác của góc B cắt AC tại D.Kẻ DH vuông góc tại BC (H thuộc BC)
a)So sánh AB và HB
b)So sánh AD và CD
Bài 2:Cho tam giác ABC có AB<AC.Tia phân giác của góc A cắt BC tại D,đường thẳng đi qua A vuông góc BC tại H
a)C/minh H thuộc tia BD
b)Cho góc B nhỏ.C/minh H nằm giữa B và D
c)Cho M là trung điểm của BC.C/minh D nằm giữa H và M
Bài 1 a, xét tam giác ABD và tam giác HBD có:
BD cạnh chung
\(\widehat{ABD}\)=\(\widehat{HBD}\)(gt)
\(\Rightarrow\)tam giác ABD = tam giác HBD( CH-GN)
\(\Rightarrow\)AB=HB
b,trên tia đối của tia DH lấy O sao cho HD=DO
xét tam giác ADO và tam giác CDH có:
DH=DO( theo trên)
\(\widehat{ADO}\)=\(\widehat{CDH}\)( Vì đối đỉnh)
\(\Rightarrow\)tam giác ADO=tam giác CDH( CH-GN)\(\Rightarrow\)AD=CD
Đúng 0
Bình luận (0)
Bài 2.Cho tam giác ABC nhọn, điểm D nằm giữa B và C sao cho AD không vuông góc với BC. Gọi H và K là chân đường vuông góc kẻ từ B và C đến đường thẳng AD.
a) So sánh BH+CKvà AB+AC
b) So sánh BH+CKvới BC
a: ΔBHA vuông tại H
=>BH<AB
ΔCKA vuông tại K
=>CK<AC
=>BH+CK<AB+AC
b: ΔBDH vuông tại H
=>BH<BD
ΔCKD vuông tại K
=>CK<CD
=>BH+CK<BD+CD=BC
Đúng 0
Bình luận (0)
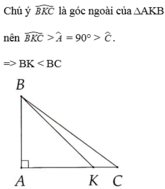
Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh độ dài BK và BC
cho tam giác abc vuông tại A .điểm I nằm giữa A và C so sánh độ dài BI và BC
góc AIB<90 độ
=>góc BIC>90 độ
Xét ΔBIC có góc BIC>90 độ
nên BC là cạnh lớn nhất
=>BC>BI
Đúng 0
Bình luận (0)