b) xét ∆ABC có AD là đường phân giác của góc A
=>BD/AB=DC/AC ( tính chất)
Áp dụng tính chất dãy tỉ số bằng nhau , được :
BD/AB=DC/AC=BD/6=DC/8=(BD+DC)/(6+8)=BD/14=10/14=5/7
==>BD=6×5:7≈4,3
==>DC=10-4,3≈5,7

a,Áp dụng định lý Pi-ta-go vào tam giác ABC => tam giác ABC vuông tại A=> AH vuông góc vs BC

=> tam giác ABC đồng dạng vs tam giác HAC ( g.c.g)

b, Vì tam giác ABC vuông tại A nên ta có hệ thức: AC²=BC . HC => đpcm

c, có AD là tia phân giác của tam giác ABC => BD=CD=BC/2= 5cm

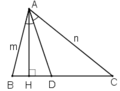
Kẻ AH là đường cao của tam giác ABC

Ta có:

Vậy tỉ số diện tích của tam giác ABD và tam giác ACD bằng m/n.

a/ Theo tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy ta có

\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{m}{n}\)

Hai tam giác ABD và tam giác ACD có chung đường cao hạ từ A xuống BC nên

\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{BD}{CD}=\frac{m}{n}\)

b/ Ta có

\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{m}{n}\Rightarrow\frac{S_{\Delta ABD}}{m}=\frac{S_{\Delta ACD}}{n}=\frac{S_{\Delta ABD}+S_{\Delta ACD}}{m+n}=\frac{S_{\Delta ABC}}{m+n}=\frac{s}{m+n}\)

\(\Rightarrow S_{\Delta ABD}=\frac{sm}{m+n}\)

Xét hai tam giác ABM và tam giác ABC có chung đường cao hạ từ A xuống BC nên

\(\frac{S_{\Delta ABM}}{S_{\Delta ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{\Delta ABM}=\frac{S_{\Delta ABC}}{2}=\frac{s}{2}\)

Mà \(S_{\Delta ADM}=S_{\Delta ABM}-S_{\Delta ABD}=\frac{s}{2}-\frac{sm}{m+n}\)

bạn ơi tại sao  \(\frac{BD}{BC}=\frac{1}{2}\) vậy bạn?

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có

AD chung

AB=AC

Do đó; ΔABD=ΔACD

a: Xét ΔABD vuông tại B và ΔACD vuông tại C có

AD chung

AB=AC

Do đó: ΔABD=ΔACD

a: Xét ΔABD và ΔACD có

AB=AC

góc BAD=góc CAD

AD chung

=>ΔABD=ΔACD

c: ΔABC cân tại A

mà AD là phân giác

nen AD vuông góc BC

Xét ΔABC có

AD,BE,CK là các đường cao

=>AD,BE,CK đồng quy

a) Xét \(\Delta\)ABD và \(\Delta\)ACD có:

        AB = AC (gt)

        AD: cạnh chung

        BD = CD (D là trung điểm của BC)

\(\Rightarrow\Delta\)ABD = \(\Delta\)ACD (c.c.c)

b) Ta có: \(\Delta\)ABD = \(\Delta\)ACD (theo ý a)

\(\Rightarrow\widehat{BAD}\) = \(\widehat{CAD}\) (2 góc tương ứng)

\(\Rightarrow\) AD là tia phân giác của \(\widehat{BAC}\)

c) Ta có: \(\Delta\)ABD = \(\Delta\)ACD (theo ý a)

\(\Rightarrow\widehat{ADB}\) =\(\widehat{ADC}\) (2 góc tương ứng)

mà \(\widehat{ADB}\) + \(\widehat{ADC}\) = 180⁰180⁰ (2 góc kề bù)

\(\Rightarrow\widehat{ADB}\) = \(\widehat{ADC}\) = 90⁰90⁰

\(\Rightarrow\) AD \(\perp\) BC

Lại có: d // BC (gt)  \(\Rightarrow\) AD \(\perp\) d

ĐS:......................

#Châu's ngốc