cho tam giác ABC có góc a lớn hơn góc b . trên cạnh BC lấy điểm H sao cho góc HAC = góc ABC . Đường phân giác của góc BAH cắt BH tại E . từ trung điểmM của AB kẻ ME cắt đường thẳng AH tại F . Chứng minh rằng CF song song với AE
Cho tam giác ABC có\(\widehat{A}>\widehat{B}.\)Trên cạnh BC lấy điểm H sao cho\(\widehat{HAC}=\widehat{ABC.}\)Đường phân giác của góc\(\widehat{BAH}\)cắt cạnh BH ở E. Từ trung điểm M của AB kẻ ME cắt đường thẳng AH tại F. Chứng minh rằng:\(CF//AE.\)
minh gợi ý theo cách của mình là:
Vì góc BAH là phân giác nên ta có:
\(\frac{AB}{BE}=\frac{AH}{HE}\) ( hãy chứng minh \(\frac{AB}{BE}=\frac{AF}{EC}\)nếu họ nói chứng minh CF ss AE thì ta có : \(\frac{AH}{AF}=\frac{EH}{EC}\)hay \(\frac{AH}{HE}=\frac{ÀF}{EC}\)) vì hai tỉ số trên cùng bằng \(\frac{AH}{HE}\)sau đó tự chứng minh ....
a) Xét tam giác BHA và tam giác BAC có
góc BHA= góc BAC (=90)
góc B chung
=> tam giác BHA đồng dạng tam giác BAC (g.g)
Cho tam giác ABC vuông tại A có AB=15 cm AC=20cm. Vẽ AH vuông góc với BC tại H.
1,Chứng minh tam giác HBA và tam giác ABC đồng dạng.
2,Tính BC, AH.
3,Vẽ tia phân giác của góc BAH cắt BH tại D. Tính BH DH .
4, Trên cạnh HC lấy E sao cho HE =HA, qua E vẽ đường thẳng vuông góc với cạnh BC cắt AC tại M, qua C vẽ đường thẳng vuông góc với BC cắt tia phân giác của góc MEC tại F. Chứng minh H,M,F thẳng hàng
cho tam giác ABC vuông tại A, đường cao AH ( AH thuộc BC ). tia phân giác của HAB cắt cạnh BC tại D, tia phân giác của góc HAC cắt cạnh BC tại E. Trên cạnh AC lấy điểm F sao cho AF=AH
a) tính số đo góc DAE
b)chứng minh tam giác AEH= tam giác AEF
c) chứng minh AB//EF
Cho tam giác ABC cân tại A, có AB=13cm;BC=10cm. Kẻ AH vuông góc BC (H thuộc BC)
a) Chứng minh HB=HC và tính AH.
b) Đường trung tuyến BD của tam giác ABC cắt AH tại G. Tính độ dài đoạn thẳng AG và BD.
c) Chứng minh tam giác BGC cân.
d) Từ B kẻ đường thẳng vuông góc với AB, đường thẳng này cắt đoạn thẳng A C tại E. Trên cạnh AE lấy điểm F sao cho EB= E F. Chứng minh góc CPF=1/2 ABE
4)Cho tam giác ABC cân tại A. Vẽ AH ⊥ BC
a)Chứng minh: ∆AHB = ∆AHC ;
b)Vẽ HM ⊥ AB, HN ⊥ AC. Chứng minh ∆AMN cân
c)Chứng minh MN // BC ;
d)Chứng minh AH2 + BM2 = AN2 + BH2
5)Cho tam giác ABC vuông tại A, có AB < AC. Trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ AH vuông góc với BC, kẻ DK vuông góc với AC
.a)Chứng minh : ADBDABˆˆ=;
b)Chứng minh : AD là phân giác của góc HAC
c) Chứng minh : AK = AH.
6)Cho tam giác cân ABC có AB = AC = 5 cm , BC = 8 cm . Kẻ AH vuông góc với BC (H ∈ BC)
a) Chứng minh : HB = HC và ·CAH = ·BAH
b)Tính độ dài AH ?
c)Kẻ HD vuông góc AB ( D ∈AB), kẻ HE vuông góc với AC(E ∈AC). Chứng minh : DE//BC
7)Cho tam giác ABC , có AC < AB , M là trung điểm BC, vẽ phân giác AD. Từ M vẽ đường thẳng vuông góc với AD tại H, đường thẳng này cắt tia AC tại F ,cắt AB tại E.
Chứng minh rằng :a) ∆ AFE cân
b) Vẽ đường thẳng Bx // EF, cắt AC tại K. Chứng minh rằng : KF = BE
c) Chứng minh rằng : AE = (AB+AC):2
8) Cho tam giác DEF vuông tại D, phân giác EB . Kẻ BI vuông góc với EF tại I . Gọi H là giao điểm của ED và IB .
Chứng minh : a) ΔEDB = Δ EIB ;
b) HB = BF
c) Gọi K là trung điểm của HF. Chứng minh 3 điểm E, B, K thẳng hàng ;
d) DI // HF
9) Cho tam giác ABC vuông tại A . Đường phân giác của góc B cắt AC tại H . Kẻ HE vuông góc với BC. Đường thẳng EH và BA cắt nhau tại I .
a)Chứng minh rẳng : ΔABH = ΔEBH ;
b)Chứng minh BH là trung trực của AE
c)Chứng minh BH vuông góc với IC . Có nhận xét gì về tam giác IBC
10) Cho ΔABC vuông tại A, M là trung điểm BC, vẽ MH ⊥AB. Trên tia đối tia MH lấy điểm K sao cho MK = MH.
a).CMR: ΔMHB = ΔMKC
b).CMR: AC = HK
c).CH cắt AM tại G, tia BG cắt AC tại I. CMR: I là trung điểm AC
11) Cho ∆ ABC cân tại A. Trên BC lấy D và E sao cho BD = CE ( D và E nằm ngoài tam giác ). Kẻ tia DI ⊥ AB,kẻ tia EK ⊥AC, DI cắt EK tại H.
a) CMR: ∆ ABE = ∆ ACD.
b) CMR: HD = HE.
c)Gọi O là giao điểm của CI và BK ;∆ OED là tam giác gì ? chứng minh.
d) CMR: AO là tia phân giác của góc BAC ?
e) A ,O , H thẳng hàng
12) Cho tam giác ABC cân ở A có AB = AC = 5 cm; kẻ AH ⊥ BC ( H ∈ BC)
a) Chứng minh BH = HC và BAH = CAH
b) Tính độ dài BH biết AH = 4 cm
c) Kẻ HD ⊥ AB ( d ∈ AB), kẻ EH ⊥ AC (E ∈ AC).
d) Tam giác ADE là tam giác gì? Vì sao?
Có ai trả lời bài 7 đi, mình cũng đang cần bài đó
Hu hu hu
Cho tam giác ABC vuông tại A, có AB = 12cm, BC = 20cm
1) Tính độ dài cạnh AC và so sánh các góc của tam giác ABC
2) Vẽ AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho H là trung điểm của đoạn thẳng AD. Chứng minh tam giác AHC = tam giác DHC
3) Gọi E,F lần lượt là trung điểm của cạnh DC,AC. Đường thẳng DF cắt HC tại M. C/m 3 điểm A,M,E thẳng hàng
4) Vẽ tia phân giác của góc BAH cắt cạnh BH tại N. C/m tam giác ANC cân và NH < NB
Cho tam giác ABC vuông tại A có AB < AC .Kẻ AH vuông góc với BC ,AD là phân giác của góc HAC (D thuộc cạnh BC ). từ D kẻ DE vuông góc với AC. Đường thẳng AH cắt đường thẳng ED tại M
a)chứng minh tam giác AHD = tam giác AED rồi suy ra BH = DE
b) Chứng minh tam giác BMC cân
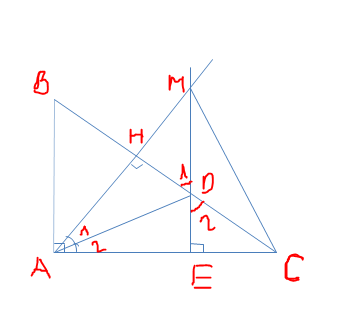
a/ Xét \(\Delta\) vuông AHD và \(\Delta\) AED. Có:
\(\widehat{A1}\)= \(\widehat{A2}\) ( giả thiết)
AD chung
=> \(\Delta AHD=\Delta AED\) ( ch-gn)
=> DH = DE ( 2 cạnh tương ứng )
b/ BMC không cân được bạn nhé. bạn chép nhầm đề bài r: Chứng minh DMC cân mới đúng.
Xét \(\Delta vuôngHDM\) và \(\Delta vuôngEDC\). Có:
\(\widehat{D1}\) = \(\widehat{D2}\) ( đối đỉnh)
HD = HE ( cmt)
=> \(\Delta HDM=\Delta EDC\left(cgv-gnk\right)\)
=> DM = DC ( 2 cạnh tương ứng)
=> Xét \(\Delta DMCcóDM=DC=>\Delta DMCcân\left(cântạiD\right)\)
~ Cậu ktra lại nhé~