cho hình chủ' nhật ABCD,E là 1 điểm trên cạnh AB;DE cắt AC tại F và cắt CB tại G
a）chú'ng minh tam giác AFE đồng dạng tam giác CFD
b）chú'ng minh FD2 ＝FE.FG
Những câu hỏi liên quan
Cho hình chữ nhật ABCD có chiêù ài là 30 cm, chiều rộng = 3/5 chiều dài. Trên cạnh AB lấy điểm M sao cho AM=1/3 * AB, trên cạnh AD lấy điểm N sao cho An = 2/3 * AB. Tính diện tích hình tam giác MNC.
Sáng nay ăn bát phở gà
Suýt thì chết sặc…. ha….ha….chít cười
Có cô vợ rất xinh tươi
Ngồi bàn phía trước nghiêng người nhỏ to
Chồng ơi vợ thấy lo lo
Cái vòng một nhỏ, nâng cho chuẩn nè
Anh chồng vẫn chén, im re
Cô vợ rụt rè khe khẽ kéo tay
Anh chồng mới nói: Vợ này !
Để nguyên đi vợ, chớ thay làm gì
Thổi phồng sự thật làm chi
Sau đó cười khì măm tiếp phở luôn.
Buông tay, cô vợ thoáng buồn
Chàng tính bài chuồn, đã thế biết tay
Chồng ơi nghe vợ nói này
Tối về đừng có giả say làm càn
Đừng hòng quen thói…. dã man
Bóp cho sự thật kêu than….méo roài.
hay thi h
Đúng 0
Bình luận (0)
Ta có: SNDC = 1/3 SADC = 1/3 . 1/2 SABCD = 1/6 SABCD
SMBC = 2/3 SACB = 2/3 . 1/2 SABCD = 1/3 SABCD
SAMN = 1/3 SANB = 1/3. 2/3. SADB = 1/3 . 2/3 . 1/2 SABCD = 1/9 SABCD
=> SNDC + SMBC + SAMN = (1/6+ 1/3 + 1/9). SABCD= 11/18 SABCD
=> SMNC = 7/18 SABCD = 7/18 . (30 . 30 . 3/5) = 210
Đúng 0
Bình luận (0)
ai giai chi tiet va ve hinh giup minh cho k
Đúng 0
Bình luận (0)
Hình chữ nhật ABCD có kích thước cạnh BC=8cm và diện tích là 96cm2. Trên các cạnh của hình chữ nhật lấy các trung điểm M,N,P,Q. Tính diện tích hình thoi MNPQ.
SOS, GIÚP E VSSSS!!!!
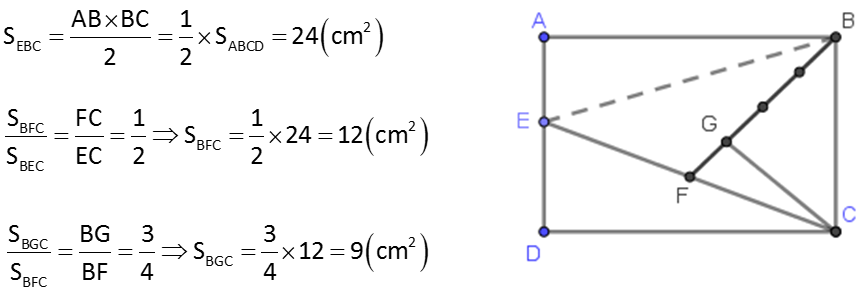
Cho hình chữ nhật ABCD. E là một điểm bất kì trên cạnh AD. Nối EC, trên cạnh EC lấy điểm F sao cho FE = FC. Nối FB, trên cạnh FB lấy điểm G sao cho FG = 1/3 × GB. Biết diện tích hình chữ nhật ABCD là 48cm2, tinh diện tích tam giác GBC.
đường cao hạ từ đỉnh E xuống đáy BC bằng đường cao hạ từ đỉnh A xuống đáy BC
đầu buồi chấm mắm tôm
Hà mai chi mất dạy mún một vé báo cáo cho thoải con gà mái ko em
cho hình chữ nhật ABCD có AB= 8 cm , AD= 6cm .trên cạnh AB,CD lần lượt lấy các điểm M,N sao cho AM=CN=3 cm
a,tính diện tích hình chữ nhật ABCD
b, tứ giác AMCN là hình gì? chứng minh. tính diện tích tứ giác AMCN.
c.giả sử AM=CN = x cm. tìm vị trí của điểm M,N trên AB,CD sao cho diện tích tứ giác AMCN bằng 1/4 diện tích của hình chữ nhật ABCD
Gấp 1 mành giấy hình chữ nhật như hình dưới đây sao cho điềm D trùng với điểm E là 1 diểm nằm trên cạnh BC . Biết AD =10 cm , AB = 8cm .Tính độ dài BE .
Có : AE = AD = 10 cm
- Áp dụng định lý pi - ta - go vào tam giác ABE vuông tại B ta được :
\(AB^2+BE^2=AE^2=AD^2\)
\(\Rightarrow8^2+BE^2=10^2\)
\(\Rightarrow BE=6\left(cm\right)\)
Vậy ...
Đúng 1
Bình luận (0)
Từ điều kiện đề bài suy ra △ADF=△AEF
⇒AE=AD=10 (cm)
Áp dụng định lý Pitago cho tam giác vuông ABE có:
BE=\(\sqrt{AE^2-AB^2}=\sqrt{10^2-8^2}=\sqrt{100-64}=\sqrt{36}=6\) (cm)
Đúng 1
Bình luận (1)
Giúp tôi với:
Cho hình vuông ABCD cạnh a, trên hai cạnh AB, AD lần lượt lấy hai điểm E, F sao cho chu vi tam giác AEF bằng 2a. M là hình chiếu của điểm C trên EF . C/M độ dài CM không đổi.
Trên tia đối của BA lấy điểm G sao cho BG=DF.
Xét tam giác CDF và tam giác CBG:
CD=CB
^CDF=^CBG=900 => Tam giác CDF=Tam giác CBG(c.g.c)
DF=BG
=> CF=CG (2 cạnh tương ứng)
=> ^CFD=^CGB (2 góc tương ứng)
Ta có: Chu vi tam giác AEF=2a =>AE+AF+EF=2a (1)
Mà a là số đo cạnh của hình vuông ABCD => 2a=AB+AD (2)
Từ (1) và (2)=> AE+AF+EF=AB+AD
<=> AE+AF+EF=AE+AF+DF+BE <=> EF=DF+BE
Lại có: DF=BG => EF=BG+BE <=> EF=EG.
Xét tam giác EFC và tam giác EGC:
EF=EG
EC chung => Tam giác EFC=Tam giác EGC (c.c.c)
CF=CG (cmt)
=> ^EFC=^EGC (2 góc tương ứng) hay ^BGC=^MFC
Mà ^CFD=^CGB => ^MFC=^CFD
Xét tam giác CDF và tam giác CMF:
^CDF=^CMF=900
CF chung => Tam giác CDF=Tam giác CMF (Cạnh huyền góc nhọn)
^CFD=^MFC
=> CD=CM (2 cạnh tương ứng) => CM=a
Mà giá trị của a không đổi (vì là số đo cạnh hình vuông)
=> Độ dài CM không ddổi (đpcm).
Đúng 0
Bình luận (0)
Kurokawa Neko làm đung
Giá trị của a ko thay đổi vì số đo cạnh góc vuông
Vậy độ dài CM ko thay đổi
Đúng 0
Bình luận (0)
Cho hình chữ nhật có ABCD, N là trung điểm của cạnh. Biết AM=12cm,MB=6cm ,BC=12cm
a,Tính diện tích hình chữ nhật ABCD
b,Tính diện tích hình tam giác MNC
a) Cạnh AB là : 12 x 2/3 = 8 (cm)
Diện tích ABCD là : (8 + 12) : 2 x 6 = 60 (cm2)
b) -Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau = 6cm mà đáy AB = 2/3 CD => S_ABC = 2/3 S_DBC.
Vẫn xét 2 tam giác ABC và DBC chung đáy BC vì S_ABC = 2/3 S_DBC => chiều cao AK = 2/3 DH.
-Xét tam giác AMC và DMC chung đáy MC mà chiều cao AK = 2/3 DH => S_AMC = 2/3 S_DMC. Mà S_DMC lớn hơn S_AMC là : 12 x 6 : 2 = 36 (cm2)
S_AMC là : 36 : (3-2) x 2 = 72 (cm2) (Toán Hiệu - Tỉ)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 x 2 : 12 = 12 (cm)
mk trả lời đầu tiên nhớ k cho mk nha!!!..
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có cạnh bằng bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB 2a, AD a. Gọi K là điểm thuộc BC sao cho
3
B
K
→
+
2
C
K
→
0
→
Tính khoảng cách giữa hai đươ...
Đọc tiếp
Cho hình chóp S.ABCD có cạnh bằng bên bằng nhau và bằng 2a, đáy là hình chữ nhật ABCD có AB = 2a, AD = a. Gọi K là điểm thuộc BC sao cho 3 B K → + 2 C K → = 0 → Tính khoảng cách giữa hai đường thẳng AD và SK.
A . x = 2 165 a 15
B . x = 165 a 15
C . x = 2 135 a 15
D . x = 135 a 15
Chọn A
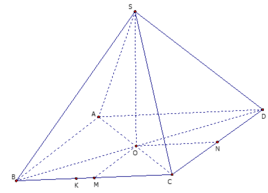
Gọi O là giao điểm của AC và BD, M là trung điểm của BC, N là trung điểm của CD.
Chọn hệ trục tọa độ Oxyz sao cho:
Đúng 0
Bình luận (0)
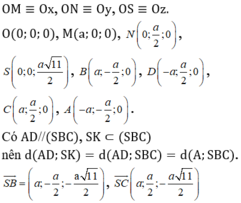
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho AE = DF
1) Chứng minh: AE // DF; BE // CF
2) Chứng minh: BE = CF
3) Chứng minh: Tứ giác AEFD là hình bình hành
4) Chứng minh: Tứ giác BEFC là hình bình hành
Có thể giải giúp mình không ạ? Mình cảm ơn
a) Vì ABCD là hình bình hành\(\Rightarrow AB//CD\)
mà \(E\in CD,F\in CD\)\(\Rightarrow AE//DF,BE//CF\left(đpcm\right)\)
b) ABCD là hình bình hành \(\Rightarrow AB=CD\)
mà \(AE=DF\left(gt\right)\)\(\Rightarrow BE=CF\left(đpcm\right)\)
c) Tứ giác AEFD có AE // DF, AE = DF
\(\Rightarrow\)Tứ giác AEFD là hình bình hành (đpcm)
d) Chứng minh tương tự phần c ta suy ra đpcm
Đúng 0
Bình luận (0)
