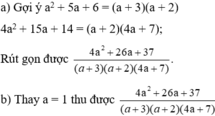a) Gợi ý: a 2 − 5 a + 4 = ( a − 1 ) ( a − 4 ) ; a 2 + 3 a − 4 = ( a − 1 ) ( a + 4 )  

Ta rút gọn được A = a + 1 a − 4  

b) Thay a = 5 vào biểu thức A tìm được A = 6

c) Ta biến đổi A = a + 1 a − 4 = 1 + 5 a − 4  

⇒ A ∈ ℤ ⇒ a ∈ − 1 ;   3 ;   5 ;   9

Ta có

f ' x = 2 a 2 - 3 cos x + 4 a cos 2 x f " x = 2 3 - a 2 sin x + 8 a sin 2 x

Hàm số f(x) đạt cực tiểu tại x = π 3  khi và chỉ khi

f ' π 3 = 0 f " π 3 > 0 ⇔ a 2 - 2 a + 3 = 0 - 3 a 2 - 4 a - 3 > 0 ⇔ a = 1

Đáp án B

Xét hiệu \(2a^2+2b^2-\left(a^3+ab^2\right)=\left(2a^2-a^3\right)+\left(2b^2-ab^2\right)\)

\(=a^2\left(2-a\right)+b^2\left(2-a\right)\)

\(=\left(a^2+b^2\right)\left(2-a\right)\)

Do \(a^2+b^2\ge0;\forall a;b\) nên:

\(2a^2+2b^2>a^3+ab^2\) khi \(\left\{{}\begin{matrix}a^2+b^2\ne0\\2-a>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2\ne0\\a< 2\end{matrix}\right.\)

\(2a^2+2b^2=a^3+ab^2\) khi \(\left[{}\begin{matrix}a^2+b^2=0\\2-a=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b=0\\a=2\end{matrix}\right.\)

\(2a^2+2b^2< a^3+ab^2\) khi \(\left\{{}\begin{matrix}a^2+b^2\ne0\\a>2\end{matrix}\right.\) \(\Rightarrow a>2\)

\(2a^2+2b^2\ge a^3+ab^2\) khi \(2-a\ge0\Leftrightarrow a\le2\)

\(a^3+6=-3a-2a^2\)

\(\Leftrightarrow a^3+2a^2+6+3a=0\)

\(\Leftrightarrow a^2\left(a+2\right)+3\left(a+2\right)=0\)

\(\Leftrightarrow\left(a+2\right)\left(a^2+3\right)=0\)

\(\Leftrightarrow a+2=0\left(do.a^2+3>0\right)\)

<=>a=-2

thay a=-2 vào biểu thức ta được \(A=\frac{-2-1}{-2+3}=\frac{-3}{1}=-3\)

Ta có : a³+6=-3a-2a²

      <=> a³+6+3a+2a²=0

      <=>(a³+2a²)+(3a+6)=0

      <=>a²(a+2)+3(a+2)=0

      <=>(a²+3)(a+2)=0

      \(\hept{\begin{cases}a^2+3=0\\a+2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a^2=-3\\a=-2\end{cases}\Leftrightarrow}\hept{\begin{cases}a\in\varnothing\\a=-2\end{cases}}}\)

Thay a=-2 vào biểu thức :

=> A= \(\frac{-2-2}{-2+3}=\frac{-4}{1}=-4\)

     \(a^3+6=-3a-2a^2\)

\(\Leftrightarrow\)\(a^3+2a^2+3a+6=0\)

\(\Leftrightarrow\)\(a^2\left(a+2\right)+3\left(a+2\right)=0\)

\(\Leftrightarrow\)\(\left(a+2\right)\left(a^2+3\right)=0\)

\(\Leftrightarrow\)\(a+2=0\)   (vì a² + 3 # 0)

\(\Leftrightarrow\)\(a=-2\)

Vậy   \(A=\frac{a-1}{a+3}=\frac{-2-1}{-2+3}=3\)

sai

a) Ta có x 6 + 2 x 3 + 3 x 3 − 1 . 3 x x + 1 . x 2 + x + 1 x 6 + 2 x 3 + 3 = 3 x x 2 − 1  

b) Gợi ý: a 3   +   2 a 2  - a - 2 = (a - 1)(a + 1) (a + 2)

Thực hiện phép tính từ trái qua phải thu được:  = 1 3

A= a^3 + 3a^2 + 3a +6

=a³+3a²+3a+1+5

=(a+1)³+5

thay a=29 vào (a+1)³+5 ta được:

(29+1)³+5=30³+5=27005

Vậy với x=29 thì A=27005

B=x^3-15x^2=75x với x=25

A= a^3 + 3a^2 + 3a +6 

A=  a^3 + 3a^2 + 3a +1+5

A=(a+1)³+5

Thay a=29 vào biểu thức (a+1)³+5,Ta có

(29+1)³+5=30³+5=27000+5=27005

=>Với a=29 Thì biểu thức A có giá trị là :27005

 k minh nha ban5612345626646564625624656737636565735667357