a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.

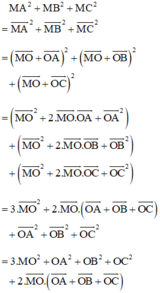
Lại có:

+ O là trọng tâm tam giác nên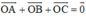 

+ Bán kính đường tròn ngoại tiếp tam giác:

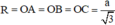
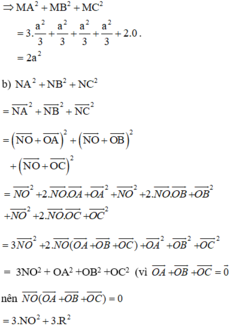
Ta có: NA2 + NB2 + NC2 ngắn nhất

⇔ NO2 ngắn nhất vì R không đổi

⇔ NO ngắn nhất

⇔ N là hình chiếu của O trên d.

Gọi cạnh tam giác là a thì \(a=R\sqrt{3}\)

Do tính đối xứng của đường tròn và tam giác đều, không mất tính tổng quát, giả sử M nằm trên cung nhỏ BC

\(\Rightarrow\widehat{BMC}=180^0-\widehat{BAC}=120^0\)

\(\Rightarrow AM.BC=AB.CM+AC.BM\Leftrightarrow AM=BM+CM\)

\(\Rightarrow S=\left(BM+CM\right)^2+2BM^2-3CM^2\)

\(=3BM^2+2BM.CM-2CM^2\)

Lại có: \(BC^2=BM^2+CM^2-2MB.MC.cos\widehat{BMC}\)

\(=BM^2+CM^2+MB.MC\Rightarrow MB.MC=3R^2-BM^2-CM^2\)

\(\Rightarrow S=6R^2+BM^2-4CM^2\)

Gọi I là điểm thỏa mãn \(\overrightarrow{BI}-4\overrightarrow{CI}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BI}=\dfrac{4}{3}\overrightarrow{BC}\)

\(\Rightarrow BI=\dfrac{4\sqrt{3}}{3}R\) ; \(CI=\dfrac{\sqrt{3}}{3}R\)

\(S=6R^2+\left(\overrightarrow{BI}+\overrightarrow{IM}\right)^2-4\left(\overrightarrow{CI}+\overrightarrow{IM}\right)^2\)

\(S=6R^2+BI^2-4CI^2-3IM^2=10R^2-3IM^2\)

\(S_{max}\) khi \(IM_{min}\Rightarrow M\equiv C\Rightarrow S=CA^2+2CB^2=9R^2\)

Hmm, sao lại không có nhỉ, thử cách khác.

O đồng thời là trọng tâm tam giác

\(S=\left(\overrightarrow{MO}+\overrightarrow{OA}\right)^2+2\left(\overrightarrow{MO}+\overrightarrow{OB}\right)^2-3\left(\overrightarrow{MO}+\overrightarrow{OC}\right)^2\)

\(=OA^2+2OB^2-3OC^2+2\overrightarrow{MO}\left(\overrightarrow{OA}+2\overrightarrow{OB}-3\overrightarrow{OC}\right)\)

\(=2\overrightarrow{MO}\left[\overrightarrow{CO}+\overrightarrow{OA}+2\overrightarrow{CO}+2\overrightarrow{OB}\right]\)

\(=2\overrightarrow{MO}\left(\overrightarrow{CA}+2\overrightarrow{CB}\right)=2\overrightarrow{MO}.\overrightarrow{CE}\)

Với E là điểm sao cho \(\overrightarrow{CA}+2\overrightarrow{CB}=\overrightarrow{CE}\)

Ta có: \(AE=CD=2BC=2\sqrt{3}R\) ; \(\widehat{CAE}=120^0\)

\(\Rightarrow CE=\sqrt{AC^2+AE^2-2AC.AE.cos120^0}=R\sqrt{21}\)

\(S=2\overrightarrow{MO}.\overrightarrow{CE}=2MO.CE.cos\left(\widehat{MO};\overrightarrow{CE}\right)=2R.R\sqrt{21}.cos\left(\overrightarrow{MO};\overrightarrow{CE}\right)\)

\(=2\sqrt{21}R^2.cos\left(\overrightarrow{MO};\overrightarrow{CE}\right)\le2\sqrt{21}R^2\)

\(\Rightarrow S_{max}=2\sqrt{21}R^2\) khi \(\overrightarrow{OM}\) cùng chiều \(\overrightarrow{CE}\)

Lần này chắc là đúng rồi, sai sót của bài làm cũ ở chỗ biểu thức S không đối xứng A; B; C nên việc giả sử M nằm trên cung nhỏ BC là sai 

Update thêm cái hình vẽ cho bạn dễ hình dung

Bài 1: 

+) Chứng minh tứ giác BFLK nội tiếp:

Ta thấy FAH và LAH  là hai tam giác vuông có chung cạnh huyền AH nên AFHL là tứ giác nội tiếp. Vậy thì \(\widehat{ALF}=\widehat{AHF}\)  (Hai góc nội tiếp cùng chắn cung AF)

Lại có \(\widehat{AHF}=\widehat{FBK}\)   (Cùng phụ với góc \(\widehat{FAH}\)  )

Vậy nên   \(\widehat{ALF}=\widehat{FBK}\), suy ra tứ giác BFLK nội tiếp (Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)

+) Chứng minh tứ giác CELK nội tiếp:

Hoàn toàn tương tự : Tứ giác AELH nội tiếp nên \(\widehat{ALE}=\widehat{AHE}\) , mà \(\widehat{AHE}=\widehat{ACD}\Rightarrow\widehat{ALE}=\widehat{ACD}\)

Suy ra tứ giác CELK nội tiếp.

Các bài còn lại em tách ra nhé.

Gọi I là tâm nội tiếp \(\Delta\)ABC, khi đó 3 điểm C,I,K  thẳng hàng. Gọi đường tròn ngoại tiếp \(\Delta\)AIE cắt tia CI tại điểm thứ hai F.

Xét \(\Delta\)CKA và \(\Delta\)CIB có: ^ACK = ^BCI (=^ACB/2); ^CAK = ^CBI (=^ABC/2) => \(\Delta\)CKA ~ \(\Delta\)CIB (g.g)

Suy ra: \(\frac{CK}{CI}=\frac{CA}{CB}\). Mà \(\frac{CA}{CB}=\frac{CD}{CA}\)(\(\Delta\)CAD ~ \(\Delta\)CBA) nên \(\frac{CK}{CI}=\frac{CD}{CA}\Rightarrow\frac{CK}{CD}=\frac{CI}{CA}\)

Lại có: CEA và CIF là 2 cát tuyến của (AIE) nên \(\frac{CI}{CA}=\frac{CE}{CF}\). Từ đó: \(\frac{CK}{CD}=\frac{CE}{CF}\)

Suy ra: \(\Delta\)CEK ~ \(\Delta\)CFD (c.g.c) => ^CEK = ^CFD. Nếu ta gọi 2 tia FD và EK cắt nhau ở L' thì ^CEL' = ^CFL'

=> Tứ giác CL'FE nội tiếp => ^ECF = ^EL'F => ^KCD = ^KL'D => Tứ giác CKDL' nội tiếp 

Áp dụng phương tích đường tròn có: FK.FC=FD.FL'   (1)

Cũng từ \(\Delta\)CKA ~ \(\Delta\)CIB (cmt) => ^BIF = ^AKI hay ^AKF = ^EIC => ^AKF = ^CAF

=> \(\Delta\)AFK ~ \(\Delta\)CFA (g.g)  => FA² = FK.FC        (2)

Từ (1) và (2) => FA² = FD.FL' => \(\Delta\)FDA ~ \(\Delta\)FAL' (c.g.c)

=> ^FL'A = ^FAD = ^DAC - ^FAC = ^ABC - ^FKA = ^ABC - (^KAC + ^ACK) = ^ABC/2 - ^ACB/2

Do đó: ^AL'E = ^FL'A + ^FL'E = ^ABC/2 - ^ACB/2 + ^ACB/2 = ^ABC/2 = ^ABE => Tứ giác ABL'E nội tiếp

Hay tia EK cắt đường tròn ngoại tiếp tam giác ABE tại L' => L' trùng L

Từ đó dễ có: ^BLC = ^ABC/2 + ^ACB + ^ABC/2 + ^BAC/2 = ^ABC + ^ACB + ^BAC/2 = 180⁰ - ^BAC/2

Vậy thì tâm của đường tròn (BLC) nằm tại điểm chính giữa cung BC chứa A của (O) (đpcm).