Xác định trọng tâm của bản phẳng mỏng AIKCD, IBK là mặt cắt

Những câu hỏi liên quan
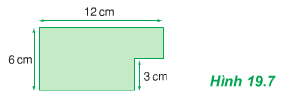
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật dài 12cm, rộng 6cm, bị cắt mất một phần hình vuông có cạnh 3cm ở một góc (Hình 19.7)
Chia bản mỏng thành hai phần.
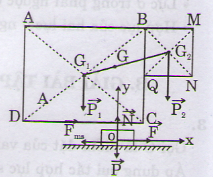
ABCD và BMNQ. Trọng tâm của 2 phần này là G1 và G2. Nếu gọi trọng tâm của bản lề G thì G sẽ là điểm đặt của hợp lực của các trọng lực P1 và P2 của hai bản nói trên.
Do trọng lượng của mỗi tấm tỉ lệ với diện tích.
Ta có: =
=
= 6
Khi đó G được xác định như sau:
=
= 6 (1)
Mặt khác ta có: G1G2 = = 6,18 cm
=> GG1 + GG2 = 6,18 (2)
(1)và(2) => GG1 = 0,882 cm
Vậy trọng tâm G nằm trên đường nối G1 và G2; cách G1 một đoạn 0,882cm
Đúng 0
Bình luận (0)
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử (α) là mặt phẳng đi qua A và vuông góc với cạnh SC, (α) cắt SC tại I.a) Xác định giao điểm K của SO với mặt phẳng (α).b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // (α).c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng (α). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (α).
Đọc tiếp
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử (α) là mặt phẳng đi qua A và vuông góc với cạnh SC, (α) cắt SC tại I.
a) Xác định giao điểm K của SO với mặt phẳng (α).
b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // (α).
c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng (α). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (α).
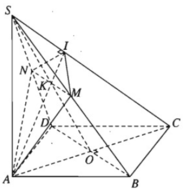
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có 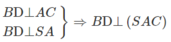
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
Đúng 0
Bình luận (0)
Một bản mỏng phẳng, đồng chất, bề dày đều có dạng như hình vẽ. Xác định vị trí trọng tâm của bản
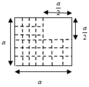
Áp dụng phương pháp tọa độ :
x G = y G = m a 4 + m a 4 + m 3 a 4 3 m = 5 a 12
Đúng 0
Bình luận (0)
Bài 5: Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O, cạnh SA vuông góc với mặt đáy. là mặt phẳng đi qua A và vuông góc với SC, cắt SC tại I.
a) Xác định giao điểm K của SO với .
b) Chứng minh: và .
c) Xác định giao tuyến của mặt phẳng và . Tìm thiết diện cắt hình chóp S.ABCD bởi .
giúp mình đc ko mọi người? em cảm ơn rất nhiều
Đọc tiếp
Bài 5: Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O, cạnh SA vuông góc với mặt đáy. là mặt phẳng đi qua A và vuông góc với SC, cắt SC tại I.
a) Xác định giao điểm K của SO với .
b) Chứng minh: và .
c) Xác định giao tuyến của mặt phẳng và . Tìm thiết diện cắt hình chóp S.ABCD bởi .
giúp mình đc ko mọi người? em cảm ơn rất nhiều
Trọng tâm của vật rắn là gì? Nêu cách xác định trọng tâm của một vật phẳng, mỏng.
á Trọng tâm của vật rắn trùng với điểm đặt của trọng lực tác dụng lên vật.
á Cách xác định trọng tâm của vật rắn:
- Trường hợp vật phẳng, mỏng có dạng hình học xác định thì trọng tâm trùng với tâm hình học của vật.
Trường hợp vật phẳng, mỏng có dạng bất kì, có thể xác định bằng thực nghiệm: Treo vật 2 lần bằng dây mảnh với các điểm buộc dây khác nhau, trọng tâm của vật là giao điểm của 2 đường thẳng vẽ trên vật, chứa dây treo trong hai lần treo đó.
Đúng 0
Bình luận (0)
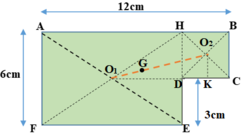
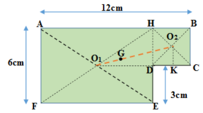
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình 19.7).
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
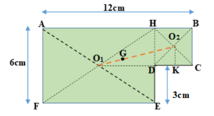
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
![]()
Gọi G là trọng tâm của cả bản phẳng ⇒ G phải nằm trền đoạn thẳng O1O2, trong đó O1 là trọng tâm của bản AHEF, O2 là trọng tâm của bản HBCD.
Ta có:
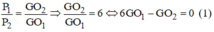
Xét tam giác vuông O1O2K ta có:
![]()
Giải hệ (1) và (2) ta được: GG1 ≈ 0,88 cm
Vậy trọng tâm G của bản phẳng nằm trên đoạn O1O2 cách O1 một đoạn 0,88 cm.
Đúng 0
Bình luận (0)
Trọng tâm của một vật là gì? Trình bày phương pháp xác định trọng tâm của vật phẳng, mỏng bằng thực nghiệm.
Trọng tâm của một vật là điểm đặt của trọng lực tác dụng lên vật đó.
Phương pháp xác định trọng tâm của vật phẳng mỏng bằng thực nghiệm:
Buộc dây vào một lỗ nhỏ A ở mép của vật rồi treo vật thẳng đứng. Khi vật nằm cân bằng, dùng bút đánh dấu phương của sợi dây AA' đi qua vật, trên vật. Tiếp theo, buộc dây vào một lỗ khác A, vào lỗ B chẳng hạn. Khi vật nằm cân bằng, đánh dâu phương sợi dây BB' qua vật.
Giao điểm của hai đoạn thẳng đánh dấu trên vật AA' và BB' chính là trọng tâm G của vật.
Đúng 0
Bình luận (0)
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ). Chọn đáp án đúng A. Trọng tâm G của bản phẳng nằm trên đoạn
O
1
O
2
cách
O
1
một đoạn 0,88 cm. B. Trọng tâm G của bản phẳng nằm trên đoạn AE cách
O...
Đọc tiếp
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ).
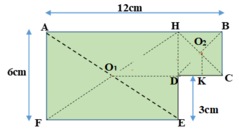
Chọn đáp án đúng
A. Trọng tâm G của bản phẳng nằm trên đoạn O 1 O 2 cách O 1 một đoạn 0,88 cm.
B. Trọng tâm G của bản phẳng nằm trên đoạn AE cách O 1 một đoạn 0,88 cm
C. Trọng tâm G của bản phẳng nằm trên đoạn BD cách O 1 một đoạn 0,55 cm
D. Trọng tâm G của bản phẳng nằm trên đoạn O 1 D cách O 1 một đoạn 0,55 cm.
Chọn A.
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
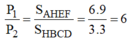
Gọi G là trọng tâm của cả bản phẳng => G phải nằm trền đoạn thẳng O 1 O 2 , trong đó O 1 là trọng tâm của bản AHEF, O 2 là trọng tâm của bản HBCD.
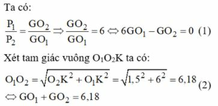
Giải hệ (1) và (2) ta được: O G 1 = 0,88 c m
Vậy trọng tâm G của bản phẳng nằm trên đoạn O 1 O 2 cách O 1 một đoạn 0,88 cm.
Đúng 0
Bình luận (0)
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ).Chọn đáp án đúng. A. Trọng tâm G của bản phẳng nằm trên đoạn
O
1
O
2
cách
O
1
một đoạn 0,88 cm. B. Trọng tâm G của bản phẳng nằm trên đoạn AE cách
O
1
một...
Đọc tiếp
Hãy xác định trọng tâm của một bản phẳng mỏng, đồng chất, hình chữ nhật, dài 12 cm, rộng 6 cm, bị cắt mất một phần hình vuông có cạnh 3 cm ở một góc (Hình vẽ).
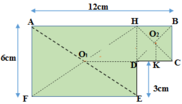
Chọn đáp án đúng.
A. Trọng tâm G của bản phẳng nằm trên đoạn O 1 O 2 cách O 1 một đoạn 0,88 cm.
B. Trọng tâm G của bản phẳng nằm trên đoạn AE cách O 1 một đoạn 0,88 cm.
C. Trọng tâm G của bản phẳng nằm trên đoạn BD cách O 1 một đoạn 0,55 cm.
D. Trọng tâm G của bản phẳng nằm trên đoạn O 1 D cách O 1 một đoạn 0,55 cm.
Chọn A.
Bản phẳng coi như gồm hai bản AHEF và HBCD ghép lại.
Biểu diễn trọng tâm các bản như hình vẽ sau:
Vì các bản đồng chất, phẳng mỏng đều nên tỉ lệ diện tích bằng tỉ lệ về trọng lượng:
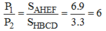
Gọi G là trọng tâm của cả bản phẳng => G phải nằm trền đoạn thẳng O1O2, trong đó O1 là trọng tâm của bản AHEF, O2 là trọng tâm của bản HBCD.
Ta có:
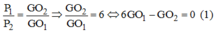
Xét tam giác vuông O1O2K ta có:
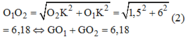
Giải hệ (1) và (2) ta được: GG1 0,88 cm
Vậy trọng tâm G của bản phẳng nằm trên đoạn O1O2 cách O1 một đoạn 0,88 cm.
Đúng 0
Bình luận (0)










