1+2+3+4...+n=9999

Những câu hỏi liên quan
Cho M=1/2*3/4*5/6*...*9999/10000 và N=2/3*4/5*6/7*...*10000/10001
a) CMR: M<N
b) CMR: M<1/100
a, Tính: M = \(1+\dfrac{1}{5}+\dfrac{3}{35}+...+\dfrac{3}{9603}+\dfrac{3}{9999}\)
b, Chứng tỏ: S = \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{4}\left(n\in N,n\ge2\right)\)
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 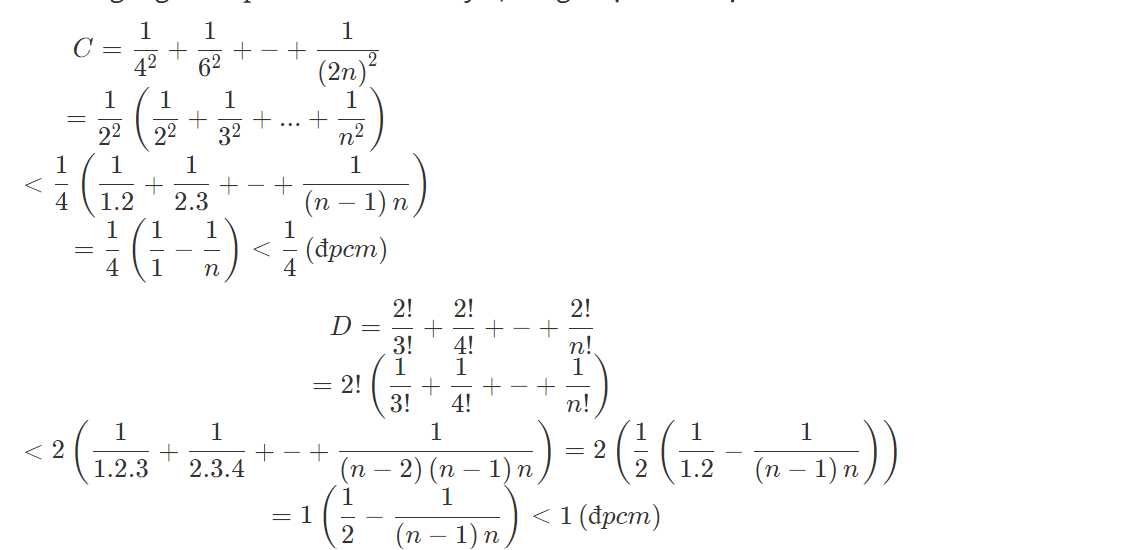
Đúng 1
Bình luận (0)
Tính giá trị biểu thức (bằng cách hợp lý nếu được)
a/ 994.114 - (10892 + 1)(10892 - 1)
b/ 99993 + 1 + 3.(99992 + 9999)
a: \(=1089^4-1089^4+1=1\)
b: \(=\left(9999+1\right)^3-3\cdot9999\left(9999+1\right)+3\left(9999^2+9999\right)\)
=10000^3=10^15
Đúng 0
Bình luận (0)
Có thể tìm được số tự nhiên n để 1+2+3+4+5+...+n=9999 hay không
tớ cần gấp đó
1+2+3+4+5+...+n=9999
<=> (n+1)n/2 = 9999
<=> n^2 +n - 19998 = 0
( không có nghiệm tư nhiên)
=> không có số tự nhiên nào thoa bài toán
Đúng 0
Bình luận (0)
1 +...+ n = n * ( n +1 ) chia 2
suy ra n *(n+1) = 3998
ko timf được số tự nhiên n nào thỏa mãn
Đúng 0
Bình luận (0)
BÀI LÀMÁp dụng công thức tính tổng dãy số tự nhiên liên tiếp ta có:
(1+n)*n/2=1999
<=> (1+n)*n=3998(nhân chéo lên)
<=> n^2 + n - 3998 = 0
Giải phương trình bậc 2 => n = 62,73 => k0 tìm được số tự nhiên n thỏa mãn đề bài
(1+n)*n/2=1999
<=> (1+n)*n=3998(nhân chéo lên)
<=> n^2 + n - 3998 = 0
Giải phương trình bậc 2 => n = 62,73 => k0 tìm được số tự nhiên n thỏa mãn đề bài
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Có thể tìm được số tự nhiên n để:
1+2+3+4+5...+n=9999 hay không?
1+2+3+4+5+...+n=9999 <=> (n+1)n/2 = 9999 <=> n^2 +n - 19998 = 0 ( không có nghiệm tư nhiên)
=> không có số tự nhiên nào thoa bài toán
Học giỏi nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1×2×3×4×5×6-6×5×4×3×2×1+9999=?
Xem thêm câu trả lời
Tính nhanh : \(\frac{10000}{10001}-\frac{9999}{10000}+\frac{1}{9999}-\frac{1}{10000}+...+\frac{3}{4}-\frac{2}{3}+\frac{1}{2}-\frac{1}{3}\)
1+2+3+4+......+9999=?
số số hạng: (9999-1):1+1=9999
tổng: (9999+1) . 9999:2=49995000
Đúng 0
Bình luận (0)





















