M nằm trong tam giác ABC
Chứng minh: a)MC+MB<AB+AC
b)MA+MB+MC<AB+AC+BC
Những câu hỏi liên quan
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.a) So sánh MB + MC với BCb) Chứng minh
M
A
+
M
B
+
M
C
A
B
+
B
C
+
C
A
2
Đọc tiếp
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.
a) So sánh MB + MC với BC
b) Chứng minh M A + M B + M C > A B + B C + C A 2
19 tháng 2 2023 lúc 10:13
Cho tam giác ABC, điểm M nằm trong tam giác. Chứng minh: MB+MC < AB+AC
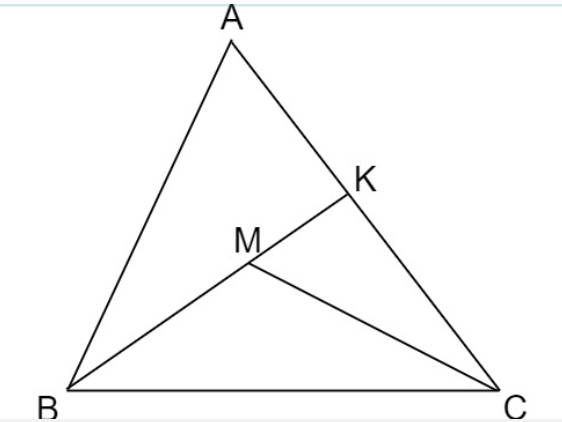
Kéo dài \(BM\) cắt \(AC\) tại \(K\)
Ta có: \(BK< AB+AK\) (bất đẳng thức t/g)
hay \(BM+MK< AB+AK\) \(\left(1\right)\)
Ta lại có: \(MC< MK+KC\) \(\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow BM+MK+MC< AB+AK+MK+KC\)
Hay \(BM+MC< AB+AK+KC\)
Hay \(BM+MC< AB+AC\)
Đúng 3
Bình luận (1)
Cho điểm M nằm trong tam giác ABC. 1) So sánh AB với MA + MB . 2) CMR: AB + AC + BC < 2(MA + MB + MC) . 3) Chứng minh rằng MA + MB +MC lớn hơn nửa chu vi tam giác ABC.
Cho tạm giác ABC . Điểm M nằm trong tam giác ABC. Chứng minh:
a,MB+MC<AB+AC
B,MA+MC<BA+BC
CHo tam giác ABC điểm M nằm trong tam giác . C/M
a) MB+ MC < AB +AC
b) C/M MA+MB+MC< chu vi tam giác ABC
Cho tam giác ABC cân tại A, điểm M nằm trong tam giác sao cho MB<MC. Chứng minh rằng góc AMB> góc AMC.
Câu hỏi của Nguyễn Hiếu Nhân - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, điểm M nằm trong tam giác sao cho MB < MC. Chứng minh rằng góc AMB > góc AMC
Trên nửa mặt phẳng bờ AC lấy điểm N sao cho \(\widehat{A}_1=\widehat{A}_2\)và AM=AN
Xét tam giác AMB và tam giác ANC có:
AB=AC(tan giác ABC cân)
\(\widehat{A}_1=\widehat{A}_2\)
AM=AN
=> tam giác AMB= tam giác ANC(c-g-c)
=>\(\widehat{M}_1=\widehat{ANC}\);BM=NC
Mà BM<MC
=>NC<MC
Xét tam giác AMN có AM=AN =>tam giác AMN cân tại A
=>\(\widehat{M}_2=\widehat{N}_2\)(1)
Xét tam giác CNM có NC<MC
=>\(\widehat{M}_3< \widehat{N}_3\)(2)
Từ (1),(2)
=>\(\widehat{M}_2+\widehat{M}_3< \widehat{N}_2+\widehat{N}_3\)
=>\(\widehat{AMC}< \widehat{ANC}\)=>\(\widehat{ANC}>\widehat{AMC}\)
=>\(\widehat{AMB}>\widehat{AMC}\)(\(\widehat{ANC}=\widehat{AMB}\))
Đúng 0
Bình luận (0)
Trên nửa mặt phẳng bờ AC lấy điểm N sao cho và AM=AN
Xét tam giác AMB và tam giác ANC có:
AB=AC(tan giác ABC cân)
AM=AN
=> tam giác AMB= tam giác ANC(c-g-c)
=>;BM=NC
Mà BM<MC
=>NC<MC
Xét tam giác AMN có AM=AN =>tam giác AMN cân tại A
=>(1)
Xét tam giác CNM có NC<MC
=>(2)
Từ (1),(2)
=>
=>=>
=>()
Cho tam giác đều ABC.Trong tam giác đều ABC lấy điểm M sao cho MB = MC và góc BMC =90 độ.
a)Chứng minh tam giác ABM = tam giác AMC
b)Trong tam giác BMC lấy điểm E sao cho góc EBC =góc ECM = 30 độ. Chứng minh tam giác MEC cân
c)Giả sử điểm M nằm trong tam giác ABC sao cho MA :MB :MC =3 :4 :5 . Tính góc AMB
mk ko bt lm câu b nha ~ xl
c,Vẽ tam giác đều AMD ( D thuộc nửa mặt phẳng bờ AM không chứa C)(Bạn tự vẽ hình nha, dễ như ăn kẹo ấy)
=> DM = AD = AM
Sau đó bạn chứng minh tam giác ADB = tam giác AMC (c.g.c) (cũng dễ thôi)
=> BD = MC (cặp cạnh tương ứng)
Ta có: DM = AM, BD = MC
=> DM : BM : BD = 3:4:5
=> tam giác BDM vuông tại M
=> góc AMB = 90o + 60o = 150o
a, Xét tam giác ABM và AMC có
BC=BA ( tam giác đều )
BMC=BMA=90độ
Góc C=A
=> ABM=AMC
Xem thêm câu trả lời
Cho tam giác ABC cân tại A, điểm M nằm trong tam giác sao cho MB < MC. Chứng minh rằng góc AMB > góc AMC
Câu hỏi của Nguyễn Hiếu Nhân - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a,m nằm trong tam giác abc,góc amb lớn hơn góc amc chứng minh mb bé hơn mc