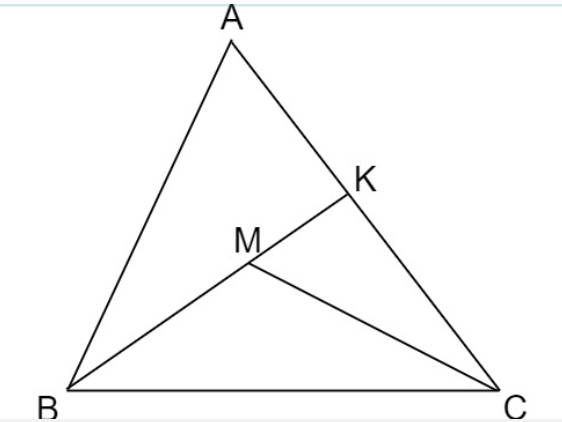
Kéo dài \(BM\) cắt \(AC\) tại \(K\)
Ta có: \(BK< AB+AK\) (bất đẳng thức t/g)
hay \(BM+MK< AB+AK\) \(\left(1\right)\)
Ta lại có: \(MC< MK+KC\) \(\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow BM+MK+MC< AB+AK+MK+KC\)
Hay \(BM+MC< AB+AK+KC\)
Hay \(BM+MC< AB+AC\)