Chứng minh đường trung trực, hoặc là hai cung nhỏ được chia ra từ điểm đó bằng nhau

a)

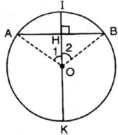
Vẽ đường tròn tâm O, dây cung AB.

Gọi I là điểm chính giữa của cung AB.

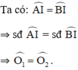
Gọi OI ∩ AB = H.

ΔAOH và ΔBOH có: AO = OB, O 1 ^ = O 2 ^  ; OH chung

⇒ ΔAOH = ΔBOH (c-g-c)

⇒ AH = BH (hai cạnh tương ứng)

⇒ OI đi qua trung điểm H của AB.

+ Mệnh đề đảo: Đường kính đi qua trung điểm của một dây cung thì đi qua điểm chính giữa của cung đó.

Mệnh đề sai

Ví dụ: Chọn dây cung AB là một đường kính của (O) (AB đi qua O). Khi đó, tồn tại đường kính CD đi qua O là trung điểm của AB nhưng C,D không phải là điểm chính giữa cung AB ( hình vẽ)

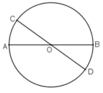
Mệnh đề đảo chỉ đúng khi dây cung AB không phải đường kính.

b)

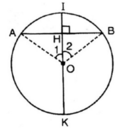
+ Cho đường tròn (O); dây cung AB ;

I là điểm chính giữa cung 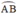 , H = OI ∩ AB.

⇒ ΔAOH = ΔBOH (cm phần a).

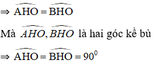
⇒ OH ⊥ AB.

Vậy đường kính đi qua điểm chính giữa của cung thì vuông góc với dây căng cung ấy.

+ Cho đường tròn (O); dây cung AB.

Kẻ đường thẳng OH ⊥ AB (H ∈ AB) cắt đường tròn tại I.

Ta có: ΔABO cân tại O (vì AO = OB = R).

⇒ đường cao OH đồng thời là đường phân giác

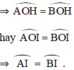
⇒ I là điểm chính giữa của cung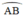 

Vậy đường kính vuông góc với dây căng cung thì đi qua điểm chính giữa của cung.

Kiến thức áp dụng

+ Điểm chính giữa cung là điểm chia cung thành hai cung bằng nhau.

a) Giả sử đường kính CD của đường tròn (O) có C là điểm chính giữa của cung AB, nghĩa là cung AC = cung CB suy ra ∠O₁ = ∠O₂

Gọi I là giao điểm của CD và AB. Khi đó OI là phân giác, đồng thời là trung tuyến của tam giác OAB (Do ΔOAB cân đỉnh O)

Vậy I là trung điểm của AB.

+ Mệnh đề đảo không đúng vì nếu dây cung AB cũng là một đường kính thì dây CD đi qua trung điểm của dây AB nhưng không đi qua điểm chính giữa của cung AB.

+ Để mệnh đề đảo chúng ta cần bổ sung thêm: Đường kính đi qua trung điểm một dây không đi qua tâm của đường tròn thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.

b) Thuận: Giả sử đường kính CD đi qua C là điểm chính giữa cung AB ⇒ cungAC = cungCB ⇒ AOC = COB ⇒ OC là tia phân giác của góc ∠AOB

Vì ΔOAB cân đỉnh O nên đường phân giác đồng thời là đường cao.

Vậy: OC ⊥ AB hay CD ⊥ AB.

Đảo: Giả sử đường kính AB ⊥ CD tại I.

Khi đó: OI là tia phân giác của góc ∠AOB ⇒ AOC = BOC ⇒ AC= BC

⇒ C là điểm giữa cung AB.

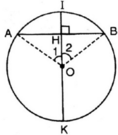
Vẽ đường tròn tâm O, dây cung AB.

Gọi I là điểm chính giữa của cung AB.

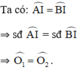
Gọi OI ∩ AB = H.

ΔAOH và ΔBOH có: AO = OB, 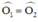 ; OH chung

⇒ ΔAOH = ΔBOH (c-g-c)

⇒ AH = BH (hai cạnh tương ứng)

⇒ OI đi qua trung điểm H của AB.

+ Mệnh đề đảo: Đường kính đi qua trung điểm của một dây cung thì đi qua điểm chính giữa của cung đó.

Mệnh đề sai

Ví dụ: Chọn dây cung AB là một đường kính của (O) (AB đi qua O). Khi đó, tồn tại đường kính CD đi qua O là trung điểm của AB nhưng C,D không phải là điểm chính giữa cung AB ( hình vẽ)

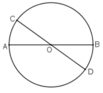
Mệnh đề đảo chỉ đúng khi dây cung AB không phải đường kính.