Cho tam giác ABC ngoại tiếp đường tròn (O). CMR: 2AD = AB + AC - BC

Những câu hỏi liên quan
Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).
Chứng minh rằng:
2AD = AB + AC – BC
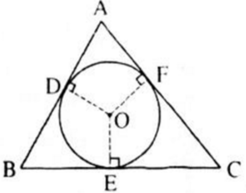
Hình 82
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
BD = BE, CE = CF, AD = AF
Ta có:
AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)
= (AD + AF) + (DB – BE) + (FC – EC)
= AD + AF = 2AD.
Vậy 2AD = AB + AC – BC (đpcm)
Đúng 0
Bình luận (0)
Trên hình 82, tam giác ABC ngoại tiếp đường tròn (O).
a) Chứng minh rằng:
2AD = AB + AC – BC
b) Tìm các hệ thức tương tự như hệ thức ở câu a).
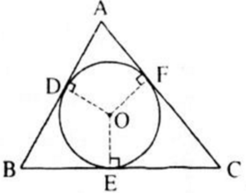
Hình 82
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
BD = BE, CE = CF, AD = AF
Ta có:
AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)
= (AD + AF) + (DB – BE) + (FC – EC)
= AD + AF = 2AD.
Vậy 2AD = AB + AC – BC (đpcm)
b) Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB,AC,BC lần lượt tiếp xúc với đường tròn tâm I tại D,F,E
a)Chứng minh rằng: 2AD= AB+AC-BC
b)CMR: các đường phân giác của tam giác ABC đồng quy tại I
c) Giả sử tam giác ABC đều và R=1cm.Tính diện tích tam giác ABC
Cho tam giác ABC có AB,AC,BC lần lượt tiếp xúc với đường tròn tâm I tại D,F,E
a)Chứng minh rằng: 2AD= AB+AC-BC
b)CMR: các đường phân giác của tam giác ABC đồng quy tại I
c) Giả sử tam giác ABC đều và R=1cm.Tính diện tích tam giác ABC
Cho tam giác ABC vuông tại A, AB=6, BC=10, AC=8. Tính bán kính của đường tròn O' tiếp xúc với AB, AC và tiếp xúc trong với đường tròn ngoại tiếp tam giác ABC
cho tam giác ABC nội tiếp đuờng tròn tâm O và đường phân giác trong AD (D thuộc BC, AC<AB). Gọi E và F thứ tự là tâm đường tròn ngoại tiếp tam giác ABD, ACD. a, CMR OE=OF; b, Đặt BC=a. TÍnh S AEOFtheo a,R
cho tam giác ABC (AB<AC) nội tiếp đường tròn (O). vẽ đường kính MN\(\perp\)BC(điểm M thuộc cung BC ko chứa A). cmr: các tia AM, AN lần lượu là các tia phân giác trong và ngoại tại đỉnh A của tam giác ABC
Cho tam giác ABC nội tiếp đường tròn tâm O đường kính AB= 2R. Trên cạnh BC lấy M ( M khác B và C), đường thẳng AM cắt (O ) ở D, E là giao điểm của BD và AC. Vẽ đường tròn (I ) ngoại tiếp tam giác MBD cắt đường kính AB ở N ( N khác B).
1. CMR: Tứ giác CEDM nội tiếp và 3 điểm E, M, N thẳng hàng 2,cho đoạn thẳng CN cắt đường tròn (i) ở F (giúp mình với ạ )
1: góc ECM+góc EDM=180 độ
=>ECMD nội tiếp
góc MNB=1/2*180=90 độ
EM vuông góc AB
MN vuông góc AB
=>E,M,N thẳng hàng
2: Đề bài yêu cầu gì?
Đúng 0
Bình luận (0)
Cho tam giác ABC , AB> AC ngoại tiếp đường tròn (I ) và nội tiếp đường tròn (O). Đường tròn (I ) tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi H là hình chiếu vuông góc của D trên EF. Đường tròn ngoại tiếp tam giác AEF cắt đường tròn (O) tại K (K khác A).
a) Chứng minh HD là phân giác của góc BHC .
b) Chứng minh ba điểm I, H, K thẳng hàng.











