cho tam giác cân ABC, có ACB =100 độ, phân giác góc A cắt BC tại D. CM: AD+BC=AB

Những câu hỏi liên quan
Tam giác ABC cân tại A . Góc BAC =100*. Tia phân giác của góc ABC cắt AC tại D . Trên BC lấy K . Góc BDK = 60*.
A, tính góc ABC,ACB
B, cm DA = DK
C, cm BC = BD+AD
Xem chi tiết
a) Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{BAC}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)
\(\Leftrightarrow\widehat{ABC}=\dfrac{180^0-100^0}{2}=40^0\)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)
hay \(\widehat{ACB}=40^0\)
Vậy: \(\widehat{ABC}=40^0\); \(\widehat{ACB}=40^0\)
Đúng 1
Bình luận (0)
Cho hình thang ABCD (AD//BC),(AD>BC) có AC vuông góc với CD,AC là tia phân giác góc BAD và ACB = 30 độ
a) CM Tam giác ABC cân tại B
b)Tính các góc của hình thang
c)Tia AB cắt DC tại I. CM Tam giác BCI đều và tam giác ADI cân tại A
d) Biết BC = 4cm tính chu vi của hình than
Bài 1: Cho tam giác cân có góc ACB= 100 độ. Phân giác trong của góc CAB cắt CB tại D. Chứng Minh AD+ DC= AB
Bài 2: Cho tam giác ABC vuông tại A. Vẽ AH vuông góc với BC tại H. Chứng minh rằng: BC2= 2HA2+ HB2+ HC2
Xét tam giác ABC vuông tại A
ta có AB2+AC2=BC2 (1)
Xét tam giác ABH vuông tại H
ta có BH2+AH2=AB2 (2)
Xét tam giác ACH vuông tại H
ta có CH2+AH2=AC2 (3)
Thay (2), (3) vào (1) ta có
BH2+AH2+CH2+AH2=BC2
BH2+2AH2+CH2=BC2
Cho tam giác ABC cân tại A có góc A = 100 độ tia phân giác của góc ABC cắt AC tại D . Chứng Minh AD + BD = BC
trên tia BC lấy M,N sao cho góc BDN=6O* , BDM=80*
CM được tam giáC BDN=BDA( g-c-g)
=> AD=DN , góc DNB=DAB=100*
=> DNC=80* = DMB
=> DN=DM =DA=MC(Tự chứng minh)
=>đpcm
Đúng 0
Bình luận (0)
Cho tam giác ABC có B =C . Tia phân giác của góc A cắt BC tại D . CMR :
a . AB = AC
b. AD vuông góc với BC
a) Xét tam giác adb và tam giác acd có
góc b= góc c(giả thiết)(1)
Cạnh ad chung(2)
Góc bad=góc cad(3)
từ (1)và(3) => góc adb=acd(4)
từ (2) (3) (4) =>tam giác abd= tam giác acd(g-c-g)
=>ab=ad( 2 cạnh tương ứng)
b)Ta có adb=adc(cmt)
mà 2 góc này kề bù => adb=adc=180độ/2=90 độ
=>ad vuông góc với bc
Đúng 0
Bình luận (0)
Cho tam gica ABC cân (AB=AC) có góc BAC=100 độ. Qua B dựng tia BX tạo với BC một góc bằng 30 độ, trong đó tia Bx nằm giữa BA và BC. Dựng tia phân giác của góc ACB cắt Bx tại I.
a, CM: tam giác CAI cân
b, tính số đo góc BAI
Câu hỏi của •Ƙ - ƔℌŤ⁀ᶦᵈᵒᶫ - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam gica ABC cân (AB=AC) có góc BAC=100 độ. Qua B dựng tia BX tạo với BC một góc bằng 30 độ, trong đó tia Bx nằm giữa BA và BC. Dựng tia phân giác của góc ACB cắt Bx tại I.
a, CM: tam giác CAI cân
b, tính số đo góc BAI
+) \(\Delta\)ABC cân => \(\hept{\begin{cases}AB=AC\left(1\right)\\\widehat{ABC}=\widehat{ACB}\end{cases}}\)
Ta có: \(\widehat{BAC}=100^o\)=> \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{BAC}}{2}=40^o\)
\(\widehat{IBC}=\widehat{ABC}-\widehat{ABI}=40^o-10^o=30^o\)
\(\widehat{ACI}=\widehat{BCI}=\frac{\widehat{ACB}}{2}=\frac{40^o}{2}=20^o\)(i)
+) Trên nửa mặt phẳng bờ AC chứa B lấy điểm K sao cho \(\Delta\)AKC đều => \(\hept{\begin{cases}\widehat{KAC}=\widehat{ACK}=\widehat{AKC}=60^o\\AK=KC=AC\left(2\right)\end{cases}}\)
=> \(\widehat{BAK}=\widehat{BAC}-\widehat{KAC}=100^o-60^o=40^o\)
Từ (1); (2) => AB=AK => \(\Delta\)ABK cân tại A => \(\widehat{ABK}=\widehat{AKB}=\frac{180^o-\widehat{BAK}}{2}=70^o\)
=> \(\widehat{KBC}=\widehat{ABK}-\widehat{ABC}=70^o-40^o=30^o\)
\(\widehat{KCB}=\widehat{KCA}-\widehat{ACB}=60^o-40^o=20^o\)
+) Xét \(\Delta\)BIC và \(\Delta\)BKC có:
\(\widehat{IBC}=\widehat{KBC}\left(=30^o\right)\)
BC chung
\(\widehat{ICB}=\widehat{KCB}\left(=20^o\right)\)
=> \(\Delta\)BIC = \(\Delta\)BKC
=> CK =CI (3)
(2); (3) => CI =CA => \(\Delta\)ACI cân tại C
b) \(\Delta\)ACI cân tại C có: \(\widehat{ACI}=20^o\) (theo (i) )
=> \(\widehat{CIA}=\widehat{CAI}=\frac{180^o-\widehat{ACI}}{2}=80^o\)
=> \(\widehat{BAI}=\widehat{BAC}-\widehat{CAI}=100^o-80^o=20^o\)
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A. Có góc A bàng 100 độ. Tia phân giác góc B cắt AC tại D. CHứng minh BC = AD + BD
cho tam giác ABC nhọn có góc A bằng 60 độ .Phân giác ABC cắt AC tại D ,phân giác ACB cắt AB tại E .BD cắt CE tại I
a, Tính số đo của góc BIC
b, Trên BC lấy F sao cho BE = BF . CM tam giác CID = tam giác CIF
c, Trên IF lấy M sao cho IM = IC+IB . CM tam giác BCM đều
a: góc ABC+góc ACB=180-60=120 độ
=>góc IBC+góc ICB=60 độ
=>góc BIC=120 độ
b: góc BIE=góc DIC=60 độ
Xét ΔEBIvà ΔFBI có
BE=BF
góc EBI=góc FBI
BI chung
Do đo: ΔEBI=ΔFBI
=>góc EIB=góc FIB=60 độ
=>góc FIC=60 độ
=>góc FIC=góc DIC
Xét ΔFCI và ΔDCI có
góc FIC=góc DIC
IC chung
góc ICF=góc ICD
Do đó; ΔFCI=ΔDCI
Đúng 0
Bình luận (0)






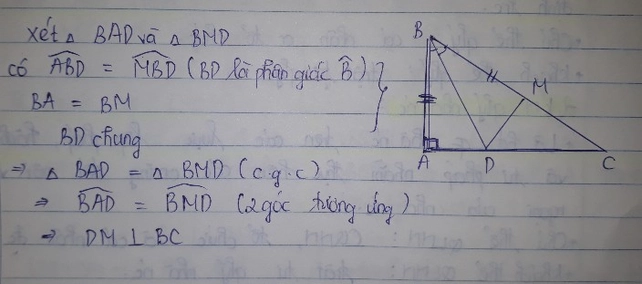 Đây là bài làm tương tự bạn tham khảo nhé!
Đây là bài làm tương tự bạn tham khảo nhé!














