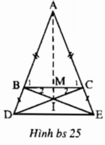
Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của AB và BC. Trên tia đối của tia BA lấy điểm D sao cho BD = BM. Trên tia đối của tia CD lấy điểm E sao cho CE = CN. Đoạn EM cắt AC ở điểm I. Chứng minh I là trung điểm của ME
GIẢI NHANH HỘ MÌNH NHÉ MỌI NGƯỜI!!!!